脉冲变压器的磁学（下）

中国法分类号：TM417文献标识码：A文章编号：0219-2713（2000）08-411-05

4高频电流效应

4．1趋肤效应

当导线流过交变电流时，在导线内部将产生与电流方向相反的电动势。由于导线中心较导线表面的磁链大，在导线中心处产生的电动势就比在导线表面附近处产生的电动势大。这样作用的结果，电流在表面流动，中心则无电流，这种由导线本身电流产生之磁场使导线电流在表面流动，就是“趋肤效应”。电流只在导线的表层流过，其表层的厚度称为“穿透厚度或趋肤深度△”，它和工作频率的平方根成反比。穿透厚度△可表示为：（21）

式中△——穿透厚度，mmK=，材料常数，铜在20℃时,K=1；

ρ—工作温度时的电阻率，Ω/cm；

ρC—铜在20℃时的电阻率=1.724×10－6，

Ω/cm；

μT—导体材质相对磁导率，非导磁材料μT=1；

f—频率，Hz；

km—与物质和温度有关的常数（例如铜：100℃时，km=75,20℃时km=65.5）

由于趋肤效应使导线有效导电面积减小，电流密度有所提高，引起铜耗增加，效率下降。因此工作于高频的变压器就需考虑这一影响。在高频变压器中的单根导线线径过大，等于浪费了铜。一般，线径不超过穿透厚度的2到3倍为宜。由式（21）可知，频率增加，穿透厚度减小。在保持电流不变的情况下，相当于电流密度增加，因此铜耗显著增大，使变压器温升增高。

4.2邻近效应

相邻导线流过高频电流时，由于磁电作用使电流偏向一边的特性，称为“邻近效应”。如相邻二导线A，B流过相反电流IA和IB时，B导线在IA产生的磁场作用下，使电流IB在B导线中靠近A导线的表面处流动，而A导线则在IB产生的磁场作用下，使电流IA在A导线中沿靠近B导线的表面处流动。又如当一些导线被缠绕成一层或几层线匝时，磁动势随绕组的层数线性增加，产生涡流，使电流集中在绕组交界面间流动，这种现象就是邻近效应。邻近效应随绕组层数增加而呈指数规律增加。因此，邻近效应影响远比趋肤效应影响大。减弱邻近效应比减弱趋肤效应作用大。

由于磁动势最大的地方，邻近效应最明显。如果能减小最大磁动势，就能相应减小邻近效应。所以合理布置原副边绕组，就能减小最大磁动势，从而减小邻近效应的影响。

理论和实践都说明，设计工频变压器时使用的简单方法，对设计高频变压器不适用。在磁芯窗口允许情况下，应尽可能使用直径大的导线来绕制变压器。在高频应用中常导致错误，使用直径太大的导线，则会使层数增加，叠加和弯曲次数增多，从而加大了邻近效应和趋肤效应，就会使损耗增加。因此太大的线径和太小的线径一样低效。显然由于邻近效应和趋肤效应缘故，绕制高频电源变压器用的导线或簿铜片有个最佳值。

5变压器的应用

变压器在电气和电子工程中被广泛应用，在长途通信和局域网（LAN）中主要用作高频开关电源的电源变压器。

信号变压器在长途通信和局域网（LAN）中的两个主要用途：作为隔离元件用和作为负载阻抗匹配用。尽管把共模扼流圈说成变压器的应用不是很精确，但共模扼流圈和变压器的工作状态有关系，所以在本文中还是把它们放在这一节来阐述。在应用双股对绞电缆的通信和局域网（LAN）中广泛采用扼流圈来抑制噪声。

5.1变压器作为隔离元件用

信号变压器应设计成允许通过信号的频率和允许的振幅失真都在一定范围之内。在长途通信和局域网（LAN）中应用的数字电路必须予以保护，使它免受外部电源，如60Hz/120V或50Hz/230V交流电的危害，50V的电话振铃信号和雷击应尽可能地接到外

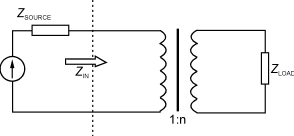
图17变压器作为阻抗匹配用

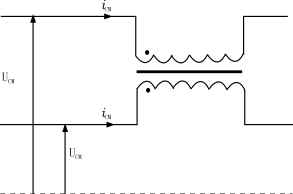
图18具有共模输入的扼流圈

接口上。在输出电路和接口之间放一个变压器可为变压器工作频率范围内的信号提供电的联系，但对这频率范围以外的信号它不起作用，局域网（LAN）和长途通信可应用的工作频率范围可以是10kHz和100MHz之间任何频率（一般来说是这样）。

频率为50Hz/60Hz的高压源信号，因为频率太低，所以无法通过信号变压器的接口。当然变压器的副边绕组会不会受到施加电源电压的危害取决于变压器的结构和功率定额。关键是原边绕组要么在长时期内、要么在危害发生之前允许的时间间隔内保持不受影响。

在雷击的情况下，变压器的副边绕组通常会损坏，但只要与原边隔离，就能达到保护的目的。

5.2作为阻抗匹配用

在2.13节中已提到负载阻抗从变压器的副边转换到原边，只要在阻抗上乘以1/n2的系数即可。变压器的这一特性，使变压器能用于对不同源和负载阻抗进行匹配。

源和负载的匹配阻抗表示为：

ZIN=ZSOURCE

从2.13节中我们知道等效阻抗是接在原边的两端（等于ZIN）。

ZIN=ZLOAD／n2

因此，输入和输出如匹配，则：（22）

5.3共模扼流圈

共模扼流圈工作和变压器相似，它也是用绕在同一磁心上的不同线圈来产生磁的耦合。它和变压器不同之处在于它不是用作信号的变换和隔离，说得确切一些，即它对加于其上的共模信号呈现高阻抗，允许差模信号不受阻碍地通过。

当共模电压加于输入端的扼流圈如图18所示，图中的基准电平是任意的。加在每一条线上的电流和电压是相等的（电流的返回通道没有画出，但实际上，它通常是通过寄生电容返回到基准电平上）。

绕在同一磁心上两个绕组的匝比是1：1，在理想情况下，所有磁通都是相互耦合的（和理想变压器一样）。在同一方向流动的两个共模电流，产生相位相同的磁通。它们产生的影响就相当于串联的感抗，它的大小取决于信号频率和线圈的参数（如磁心截面和磁导率等）。

当差模电压加于输入端的扼流圈如图19所示，总的合成电流流过负载通过扼流圈返回。在扼流圈中流过相反方向的电流磁通相互抵消。扼流圈对差模信号实际上是“觉察不出的”。

上面叙述的完美扼流圈具有无限宽的频率响应，对共模信号呈现无限大的阻抗，对差模信号阻抗为零。实际的扼流圈和变压器一样除有绕组电阻外还有漏电感、分布电容和磁心损耗。它产生的效应，除了对差模信号有不等于零的阻抗外，它的频率响应也是有限的、共模阻抗也是有限的。

一般来说，共模扼流圈的工作频率与它的共模电感成反比。

6变压器的测试

测量图16所示变压器等效电路参数，通常是为了验证要求的计算值。两种简单的测试能确定导出的参数。

6.1开路测试

这种测试通常是在低频下进行的，所以变压器的电容项可以忽略。这种测试电路如图20所示。

变压器额定电压常加在原边线圈端子上。副边线圈开路，所以副边没有电流流动、副边没有漏电

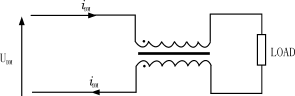
图19具有差模输入的扼流圈

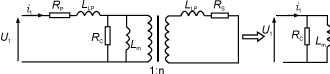
图20开路测试

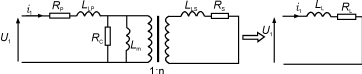
图21短路测试

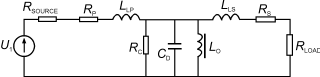
图22具有电源和负载的等效电路

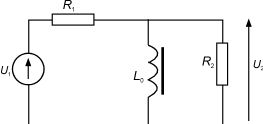
图23低频等效电路

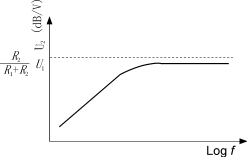
图24低频响应

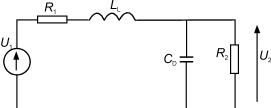
图25高频等效电路

感、副边绕组可以忽略。通常，原边漏感和电阻比励磁电感和磁心损耗等效电阻小得多，也可以忽略。简化等效电路如图20右边所示。测量所加电压和由它引起电流的幅值和相位就能得出励磁电抗和磁心损耗等效电阻。现代阻抗电桥能完成必需的计算并以数字方式直接给出电感和电阻的测量值。

因为在测试中励磁电感是在副边绕组开路情况下测得的，所以一般称之为开路电感（LO或OCL），在本文中将始终使用这一专门术语。

6.2短路测试

再一次忽略绕组内部的电容，得到的测试电路如图21所示。

副边线圈是短路的，使额定电流流过原边绕组的端点上。由于短路电压U1很小，开路电感和磁心损耗等效电阻要比副边开路时小得多，所以能被忽略。短路测试最终等效电路如图21右边所示。折合到原边的将是漏电感和绕组电阻的测量值（见2.13节）。测量原边的电压和电流的幅值与相位就能得出电感和电阻值（LL=LLP＋LLS/n2,RL=RP＋RS/n2）。

绕组电阻的测量也可以直接用直流电压加在原边或副边绕组进行测量。测得的电阻就是每个绕组的直流电阻（DCR）。

7频率响应特性

下面用第3节变压器的等效电路和有关的简化假设去描述一般宽带信号变压器的频率响应曲线。在感兴趣的频率范围内，绕组之间的电容假设可以忽略。

我们可画出变压器接有电源和负载（假设两者都是纯电阻性的）的等效电路，并对它作进一步简化得出的等效电路如图22所示，图中负载电阻，副边的漏感和副边绕阻电阻全部换算成理想变压器原边的元件。

7.1低频响应

在低频时，对图22等效电路作出进一步简化是可能的：

（1）CD的阻抗值足够大，可以忽略；

（2）RSOURCE和RP可合并为一原边电阻R1。

RP?RSOURCE；

（3）RLOAD，RC和RS可合并为一电阻R2。

RS?RLOAD，RC?RLOAD；

（4）漏感电抗足够小，可以忽略。

在上述假设下，画出的低频等效电路如图23所示。U2和负载两端的电压非常接近。L0的阻抗（开路电感）和频率f成正比。当频率f减小时，R2和L0并联的阻抗也减小。当f?0时U2?0，如图24所示。

低频响应主要是开路电感作用。当开路电感增加，低频响应就能得到改善。

7.2高频响应

在高频时可按下面的假设对图22作进一步的简化：

（1）开路电感L0的阻抗足够大，可以忽略；

（2）RSOURCE和RP可合并为一原边电阻R1。

RP?RSOURCE；

（3）RLOAD，RC和RS可合并为一电阻R2。

RS?RLOAD，RC?RLOAD

（4）漏电感可以集中在一起。

在上述假设下，我们能画出其高频等效电路如图

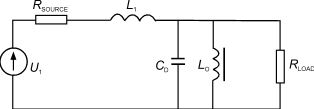
图28等效电路的时域响应

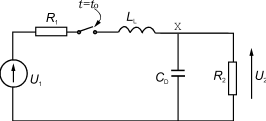
图29上升沿等效电路

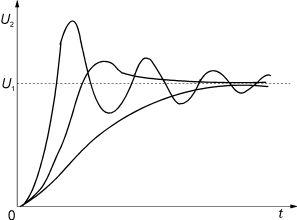
图30上升沿的波形

25所示。U2和负载两端的电压非常地接近。LL的阻抗和频率f成正比。CD的阻抗和频率f成反比。两者引起的效应是：当f?∞则U2?0，如图26所示。

高频响应主要是漏电感和分布电容起作用。当这些参数值很低时，就能得到比较好的高频响应。

7.3运行的频率响应

在理想的情况下，变压器的运行区间在它频率范围之内，变压器就相当于一个理想元件。,如果RSOURCE?RLOAD则U2=U1

在实际等效电路参数下，会使输出电压减小一些，这种衰减通常用插入损耗（dB）来表示。

插入损耗（dB）=10log（U2/U1）

　　综合7.1～7.3节可得到图27所示的频响曲线。

8时域响应特性

图32脉冲平顶响应

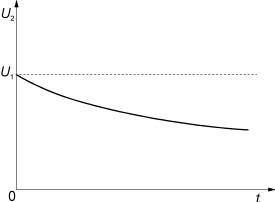
图31脉冲平顶响应的等效电路

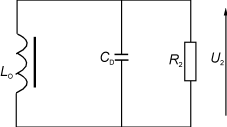
图33下降沿等效电路

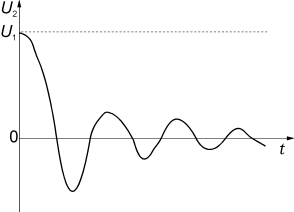
图34下降沿的响应

图35变压器的脉冲响应

本节将给出一个简单脉冲变压器的时域响应特性的简单说明。完整的含有许多方程分析起来相当复杂，为了简化分析，在本节中做下列假设：

（1）绕组电阻和源电阻及负载电阻相比是可以忽略的；

（2）漏电感可以集中在一项里；

（3）磁芯损耗电流和负载电流相比可以忽略；

（4）绕组之间的电容效应可以忽略。

这些假设对大多数实际情况来说是可行的，不会改变所获得基本特性的数据。在此假设下，可把图22的等效电路简化成如图28所示。

8.1脉冲上升沿响应

等效电路如图29所示。对于瞬间变化的输入电压而言，加在它上面的开路电感的阻抗是趋向无限大，可以忽略。假设源电阻R1也可忽略。

在此假设下，计算节点X的电流，并通过对它的方程求导数就能得到二次微分方程：这个方程的解是：

U2=U1(1＋Ae－αt＋Be－βt)(23)

图27变压器的频率响应

图26高频响应

由这个方程得出的波形如图30所示。超调量和波形的上升时间取决于R2，L2和CD的值。

8.2脉冲平顶响应

在脉冲上升沿的过渡过程结束后，就进入理想脉冲的第二阶段，脉冲平顶响应部分。其等效电路如图31所示。漏电感远小于开路电感，可以忽略。在脉冲峰值持续期间分布电容上电压的变化率是很小的，通过它的电流比负载电流很小，所以它也可以忽略。

在此假设下，我们再一次计算电流，并通过它的方程对时间求导数，就能得到一次微分方程：此方程的解是：

负载电压离开初始值后按指数规律下降，如图32所示。下降速率和开路电感成反比，即开路电感L0数值愈大，在脉冲持续期间，负载电压偏离初始值就愈小。

8.3脉冲下降沿响应

等效电路如图33所示。漏感通常比开路电感小，可以忽略。

在此假设下，先计算电流，然后再通过它对时间求导数，可以得到二次微分方程：此方程的解是：U2=U1(Aeαt＋Beβt)

　　波形的形状取决于开路电感和CD的数值。

如果磁芯的励磁电流可以忽略，则其衰减的波形，一般来说是指数衰减的阻尼正弦振荡，如图34所示。

如果忽略了过大的励磁电流，随着磁场的衰减，将会发生一个再生电动势，引起一个很大的下冲。

综合8.1和8.3节的结果，就能得到完整的脉冲响应曲线，如图35所示。为了清楚起见，图中的过渡过程和下降的峰值是被放大了的，在一个好的变压器设计中，这些将是很不显著的。

参考文献

1张占松，蔡宣三.开关电源的原理与设计.北京：电子工业出版社，1998

2叶治政,叶靖国.开关稳压电源.北京：高等教育出版社，1989