一种新颖的完全断续箝位电流模式功率因数校正电路

摘要：提供了一种新颖的宽输入范围、完全DCM、箝位电流工作模式的Boost功率因数校正电路控制方法。该控制方法不存在Boost电路中二极管的反向恢复，从而提高了整个电路的效率，同时，该方案获得了低的总谐波畸变（THD）和较高的功率因数（PF）。该方案适合于中低功率场合的应用。给出了具体的理论分析和一个100W的电路实验数据。

关键词：电流箝位升压；功率因数校正；完全断续电流模式

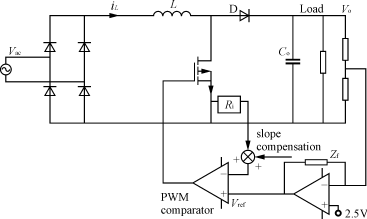
0    引言

    在以往的有源功率因数校正电路拓扑中，一个带乘法器的控制芯片不可避免。为了降低成本，一种电流箝位（Clamped Current Boost,CCB）的控制方法可以简化电路。在这种电路中，每半个周期中开关电流峰值被箝位至一个参考值。输入电流的波形跟随输入电压，这样就可以得到理想的THD。由于它不需要乘法器来提供一个电流参考值，而可以利用任何一种峰值电流控制的芯片（如UC3843）来完成这个功能，从而大大降低了成本，简化了电路。

    但是，以往提出的箝位电流模式电路，在低输入电压时工作在断续电流DCM，在高输入电压时工作在连续电流模式CCM。而CCM的工作方式存在两个缺点：一是电路中的续流二极管的反向恢复，这降低了电路的效率；二是电路中的电感值比较大，这给提高电路的功率密度带来了困难。

    本文提出了一种在通用的整个输入电压范围内工作在DCM的CCB PFC电路。该电路消除了二极管的反向恢复问题，从而提高了电路的工作效率；同时，由于工作在电流断续模式，电感量减小，这样就可以减小电感的体积，提高功率密度。

    本文给出了该电路拓扑的数学分析并且给出了一个100W的电路实验结果。

1    理论分析

    电路原理图如图1所示。在进行分析之前，假设以下条件成立：

    ——所有的元器件都是理想的；

    ——变换器工作在稳态时，开关频率远大于交流母线的频率，从而可以认为在一个开关周期内，输入电压是恒定的；

    ——输入电压是理想的正弦波v_ac=V_msin(ω_Lt)，其中ω_L为交流母线的频率；

    ——参考电压在一段时间内是一个恒定值V_ref；

    ——输出电压是恒定的。

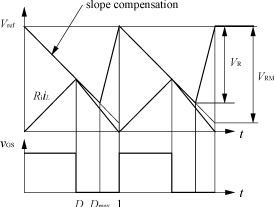
图1    CCB PFC电路

    为了便于分析，使得计算的结果与具体的电路参数无关，我们采用标幺值，即令

    V_b=V_o；

    I_b=V_o/R_t(R_t=2L/T_s，T_s为开关周期)；

    则输入的电压峰值为：

    V_m=V_m/V_b（1）

    与传统的CCB PFC电路不同，在整个母线电压输入周期内，该电路工作在电流断续模式。在每半个周期内，有两种电流断续工作模式。如图1所示，在开关周期开始阶段，Boost电路中的开关管处于开通的状态，电感中的电流i_L从零开始增加。在采样电压（R_ii_L）达到参考电压（V_ref）和斜率补偿电压（V_R）的和,或者达到最大占空比时，开关管关断，电感电流线性减小（如图2）。这两种工作模式分别定义为DCM₂和DCM₁。

(a)    DCM₁(D=D_max)

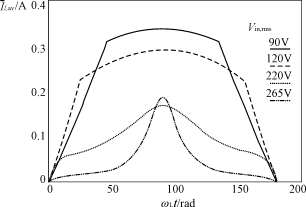
(b)    DCM₂(D<D_max)

图2    两种电流断续工作模式

    对一个周期内电感电流求平均值，可以得到两种DCM工作模式下的电流归一化后的表达式分别为：

    i_L,avDCM1=（2）

    i_L,avDCM2=（3）

式中：K_r为电流模式斜率补偿深度系数。

    DCM₁和DCM₂的边界条件为：

    D==D_max（4）

式中：斜率补偿M_c=I_R/(D_maxT_s)，I_R为斜率补偿电流。

因此，可以得出DCM₁和DCM₂两种工作模式的边界点为：

        ω_Lt=arcsin

式中：为斜率补偿电流峰值。

    由前所述，可以得到每半个周期的平均电流归一化暂态值：

    i_Lav(ω_Lt)=（5）

    由上面的分析可以得到每半个工频周期，在不同输入电压下，输入电流的的波形如图3所示。

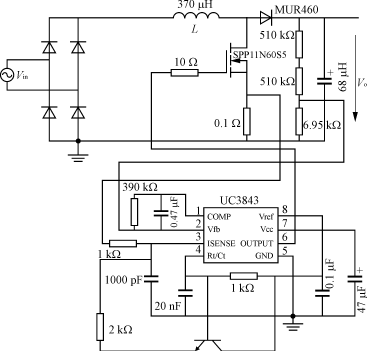
图3    输入电流波形与输入电压的关系图

    Boost电感值必须保证在整个周期内，电路工作在DCM模式。

    在最小输入电压下的电流峰值为：

    I_inp=P_o/(ηV_in,rms,min)（6）

式中：P_o为输出功率;

            η为最低效率;

      V_in,rms,min为最低的输入电压幅值。

所以，电感值由式（7）决定。

    (V_inpmin/L)D_lminT_s>=2I_inp（7）

式中：V_inpmin为最小输入电压峰值；

    D_lmin为在最小输入电压时的最小占空比，即

    D_lmin=(V_o－V_inpmin)/V_o（8）

输出电容必须满足式（9）。

    C_o>=P_o/(2πf_lineV_oΔV_o)（9）

    标幺化的功率因数可以由式（10）获得。

    PF=P_in/(V_inrmsI_inrms)（10）

式中：

    P_in=V_m|sin(ω_Lt)|i_Lav(ω_Lt)dω_Lt（11）

    =（12）

    V_inrms=V_m/（13）

那么,

    I_i,k=(i_LavDCM₁sin(kω_Lt)dω_Lt＋i_LavDCM₁sin(kω_Lt)dω_Lt

    ＋i_LavDCM₁sin(kω_Lt)dω_Lt（14）

    THD=，k=3,5,...(2N＋1)（15）

2    实验结果

    设定以下工作条件：

    V_m=127～311V；f_line=50Hz；V_o=380V；

    P_o=100W；η=0.92；f_s=77kHz；D_max=0.95。

    参数设定为：

    L=370μH；K_r=0.22；C=68μF，选用68μF/400V铝电解电容。

    电路图如图4所示。

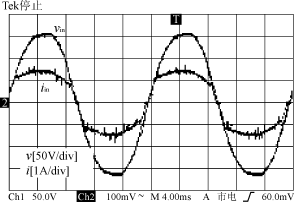
图4    实验电路图

    获得的电路波形如图5所示，由图5可以看出，实验结果符合理论分析。

(a)    V_in=90V

(b)    V_in=120V

(c)    V_in=220V

(d)    V_in=265V

图5    实验电路波形图

    表1为实验获得的PF和THD与V_in,rms关系。由表1可以看出，该电路符合IEC-3-2的标准。

表1    PF，THD与输入电压关系表

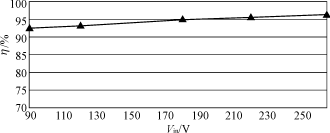
    该电路在满负载(V_o=380V，I_o=0.263A)下的效率测试如图6所示。

图6    满负载、不同电压下的电路效率

3    结语

    本文对一种在通用的整个输入电压范围内实现DCM CCB PFC的电路拓扑，进行了详细的理论分析，实验结果证明了该电路可以满足IEC1000-3-2标准。同时，由于它消除了二极管的反向恢复，采用电流断续模式，提高了电路的工作效率和功率密度。这对于中小功率的应用有很大的吸引力。