同杆双回线环流量的行波特点
本文对存在复杂耦合关系的同杆双回线分解成解耦的同向模网和环流模网的过程进行了理论推导,得到的双回线环流模网具有不包含双回线以外的系统且两端电压为零的特点,该特点使得环流网成为双回线最佳的故障定位网络,从而使复杂的双回线测距简单化。通过对比单相接地故障时双回线环流网与双回线故障线的α模行波的仿真波形,得出了双回线环流量行波和双回线路以外系统无关,且在两端母线处的反射最强在故障点的反射较弱等特点。这些特点使得基于双回线环流量的单端行波测距具有双端测距效果。本文为环流量行波用于同杆双回线测距奠定理论基础。
关键词:同杆双回线;环流量;行波
The travelling wave characterisTIcs of differenTIal component on parallel transmission lines
SONG Guo-bing, SUONAN Jia-le, XU Qing-qiang, ZHANG Jian-kang, KANG xiao-ning
(Dept. of Electric Engineering, Xi'an Jiaotong University, Xi'an 710049, china)
Abstract: A theoreTIcal derivaTIon process about complicated coupling parallel transmission lines on the same tower decomposing into decoupling common component mode nets and differential component mode nets is given in this paper, and obtained differential component mode nets have features that the nets have no relation to systems outside the parallel transmission lines and their two terminals voltage are zero. Above mentioned features make differential component nets become the optimal fault location network, and cause the complicated parallel transmission line fault location simplification. Comparing the α module travelling wave of parallel transmission line on the same tower with that of fault line by single phase earth fault, some conclusions are reached such as the differential component travelling waves are free from the systems outside the parallel transmission lines, and have strong reflection in two terminal bus bar and weak reflection at fault point. These features are beneficial to travelling wave fault location, and so as to the one-terminal travelling wave fault location based on differential component of parallel transmission lines has the same effect as two-terminal. The paper will lay a theoretical foundation for differential component used to traveling wave fault location of parallel transmission line on the same tower.
Key words: parallel transmission lines on the same tower; differential component; travelling wave
0 引言
由于同杆双回线输电技术采用双回线路共用杆塔,具有占地少,节省出线走廊等优点,故有利于环境保护,减少资金投入和缩短建设工期。因此这种输电技术越来越受到重视,并逐渐成为电能传输的主要方式。高压远距离输电线路走廊复杂,巡线困难且费用较高,因此其故障定位技术一直是电力工作者的重要研究课题。
由于同杆双回线路存在线间互感、故障类型多且复杂,尤其是在考虑同杆双回线的分布参数模型时,反应单端电气量的工频量准确故障定位问题一直没有得到很好的解决。在反应暂态电气量的行波测距方面,国内学者进行了大量的研究[3,5,7],但同杆双回线的特殊结构使得其单端行波故障测距目前也仍存在如下问题:反应单端电气量的行波测距是通过检测故障点产生的初始行波到达检测点的时间和检测点与故障点间的首次反射行波到达检测点的时间间隔实现测距。初始行波一般可以做到准确检测,但反射波中包含背侧系统复杂的反射波、故障点的反射波、对端母线和系统的反射波、故障点内部产生的反射波,因此反射波的识别非常困难,并且从理论都没解决其识别的机理,从现场得到的故障时的行波数据和仿真数据看波形复杂很难用计算机自动识别反射波进行故障测距,需由专家根据情况估算出故障点,测距可信度和成功率不高。
目前的同杆双回线故障行波测距是直接采用单回线的行波测距方法,没有反应同杆双回线自身的故障特征。通过对同杆双回线故障分析的研究发现,双回线中的电流可以分解为同向量和环流量,其中环流量仅在双回线路内部流动和系统无关,故双回线环流量中的行波不受双回线路以外的系统接线情况的影响。环流量行波仅在线路内部来回反射,测量点的行波将具有极强的规律性,且双回线环流量 行波具有行波模量高,行波波头清晰等特点。基于双回线环流量的单端行波测距具有与双端行波测距完全相同的性能,与双端行波测距相比又无须同步装置和通道配合,具有一定的应用前景。
1 同杆双回线的环流量
同杆架设的双回线路是一种并联运行状态,由于线路参数相同,在非故障状态下,两回线路的同名相流过的电流大致相等,但故障情况下,故障相的电流和另一回线同名相的电流差异很大,如果将双回线中的电流分解成同相量和环流量(与同向量相对应也称反向量[1,2,4,5,6]),则环流量只在故障时出现,且只在双回线路内部流动。以上分析表明双回线的环流量具有如下特征:①标识故障,即仅在故障时出现,能够区分故障与非故障;②只在双回线路内部流动,与双回线以外的系统参数无关,即不受双回线路以外的系统参数的影响;③双回线的环流电压沿线分布,故障点最高,双端母线侧为零。环流量的以上优良特性,使得环流量成为双回线最佳的故障识别与定位的电气量。
由前分析知,如果将双回线系统中的电压和电流表示成同向量和环流量形式[4,6],则有:

其中T为同向量,F为环流量,Ⅰ为双回线的回线1,Ⅱ双回线的回线2。为分析方便,将同杆双回线耦合关系示于图1。

如果将同杆双回线的输电线看成均匀传输线,在考虑同杆双回线间的互感和线间电容时,其传输线方程为:


其中:Ls为单位线路的自感;Lm为单回线内单位线路的线间互感;L′m为两回线间单位线路的线间互感;Cs为单位线路的对地电容;Cm为单回线内单位线路的线间电容;C′m为两回线间单位线路的线间电容。
按(1)(2)两式的变换规则,将(3)(4)两式变成同向量和环流量的传输方程:


从(5)-(8)两式表示的同向量和环流量表示的传输线方程可以看出,用同向量和环流量表示的双回线已实现两回线间解耦。然后将同向量和环流量表示的传输方程进行相模变换以消除其非对角元素,则得同向量和环流量的α模、β模、0模的模量传输线方程如下:
式 (9)、(10)式对x求偏导,并将(11)、(12)式代入,则得到如下波动方程:



式(9)、(10)对x求偏导,并将式(11)、(12)代入则得到如于波动方程:

其中:j=α、β、0。
这样,存在复杂耦合关系的同杆双回线传输线方程就分解成为六个相互独立的、彼此之间没有耦合的模量传输线方程,进而化成波动方程形式。由上述推导可以看出,所得到的不同模量下的传输参数是不尽相同,这说明分解后的不同模量具有不同的波阻抗和波速度。
上述处理过程只是将系统中的双回线部分分解成了同向量模量和环流量模量,如果将整个系统分解成为同向模量和环流模量,还需要对双回线以外的系统进行分解[4,6]。为了阐述方便,我们将上述分解得到的双回线各独立模量下的阻抗传输参数称为模阻抗,由模阻抗组成的图(与序网图对应)称之为模网图。
由(1)式可知,在双回线的母线侧,环流量电压为零,而同向量电压不为零。这说明双回线母线处因为环流量电压为零相当于直接接地,环流量模网图的模阻抗参数只含有双回线部分,双回线以外的部分在环流量模网图中将不存在;而同向量电压在双回线母线侧电压不为零,这样同向量模网图中双回线母线背侧的系统参数不能省去,在画模网图时,需要将双回线母线背侧的系统参数增加一倍[4],然后进行对应的模变换。
图2、3为将一双电源的双回线系统分解成同向量和环流量模网图。下图中双回线部分各模量下的具体线路传输参数计算分别如(9)-(12)式所示。


由以上模网图也可以看出,图2的同向量模网中双回线背侧的系统参数依然存在,故电流行波在到达M端和N端后其反射和折射将受双回线路背侧系统参数的影响。同向量模网中的行波传输和单回线相同。而图3的环流量模网中双回线背侧没有参数,行波到达M端和N端时将出现全反射,故行波在其中的传播不受双回线路背侧的系统参数影响,故其行波特征将优于单回线。
2 仿真验证
为验证同杆双回线环流量的行波特点,本文采用如图4所示的仿真模型。500kV电压等级双电源系统,线路全长110公里,中间90公里为同杆双回线,在线路发生单回线故障利用ATP进行仿真。

系统等效参数如下:
M端的系统参数:正序阻抗ZM1=j60.00Ω;零序阻抗ZM0=j46.80Ω。
N端的系统参数:正序阻抗ZN1=j45.20Ω;零序阻抗ZN0=j22.01Ω。
在仿真时,暂态数据的采样频率500kHz,即每2μs记录一个数据;记录数据长度为1000个,即只记录故障最初的2数据;以下所给的仿真结果分别是双回线故障线路行波的模和双回线环流量行波的模(它们的传播速度为259591km/s);所给出仿真波形的测点都选在M侧;另外,本文只给出了单回线故障中的单相接地故障的仿真。
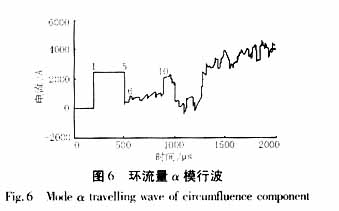
1) 金属性接地,故障发生在距M侧50km处,如图5、图6所示。

2)过渡电阻500Ω,故障发生在距M侧50km处,如图7、图8所示。


现在对以上仿真结果进行分析如下:在图5-8中的行波波头1对应故障点行波在双回线M端母线第一个反射波到达测点的时刻;波头2、3、4对应M背侧线路末端的第一、二、三个反射波到达测点的时刻;波头5对应故障点在N侧母线的第一个反射波达测点的时刻;波头6分别对应故障点与M侧母线间的第二个反射波到达测点的时刻、波头5在M背侧线路末端的第一个反射波到达测点的时刻、波头5在N背侧线路末端的第一个反射波到达测点的时刻,三者极性相同,互相叠加;波头7、8、9分别对应波头5在M和N背侧线路末端的第二、三、四个反射波到达测点的时刻,由于M和N的背侧线路都为10公里,所以二者总是同时到达,且极性相同、互相叠加;波头10、12分别对应波头1在M端和N端母线间经第一、二次反射后,到达M端测点的时刻;波头11、13分别对应波头5在M端和N端母线间经第一、二次反射后,到达M端测点的时刻。
从仿真结果可以看出:(1)双回线故障回线行波在波头1与5、5与10间包含有M、N母线背侧线路传来的折射波,而反模网中没有M、N母线背侧线路传来的杂波。(2)波头1、5间的时刻可用于行波测距,测距原理同双端行波测距。(3)双回线M、N母线处电流波为全反射。(4)波头1、10、12间的距离为双回线全长的2倍;波头5、11、13间的距离也为双回线全长的2倍;它们间隔周期出现,规律性强。
通过上述分析,可以将双回线环流量的行波特点简单归纳如下:①双回线背侧的反射波被消除;②本侧和对侧的母线反射最强烈;③故障点的反射较弱。所以可以通过本侧母线和对侧母线强烈的周期反射波来实现故障测距。
在利用双回线的环流量行波进行单端测距时,其原理和单回线的双端行波测距类似:要利用故障点行波在本侧母线的第一个反射波,和故障点行波在对侧母线的第一个反射波。在图6和图8中,如果令环流量行波的第一个上跳时刻(时刻①)为tu,第一个下跳时刻(时刻⑤)为td,行波的传输速度为v,故障点和测量点的距离为x,双回线路线长为l,则有测距方程:x=l-0.5v(td-tu)。
3 结论
同杆双回线环流量的行波具有不受双回线以外系统参数影响的特点,在本侧和对侧的行波都具有全反射的特征。故此,利用双回线环流量进行单端行波测距,在测距特点上相当于双端行波测距,且无需同步装置和通道辅助,故具有一定的现实意义和推广价值。
参考文献
[1] 索南加乐,葛耀中,陶惠良,等((SUONAN Jia-le, GE Yao-zhong, TAO Hui-liang, et al).同杆双回线的六序选相原理(The Micro-processor Based Fault Phase Indicator for the Double Circuit Line on the Same Tower Using Six Sequence Components)[J].中国电机工程学报(Proceedings of the CSEE),1991,11(6):1-9.
[2] 索南加乐,葛耀中(SUONAN Jia-le, GE Yao-zhong).用六序复合序网法分析同杆双回线的一些特殊问题(Analyzing the Special Problems of Double Circuit Lines on the Same Tower Using Six Sequence composite Sequence Nets )[J].继电器(Relay),1991,19(1):2-14.
[3] 徐丙垠(XU Bing-yin).利用暂态行波的输电线路故障测距技术,博士学位论文(Fault Location Technology of Transmission Lines based on Travelling Waves, Ph.D. Thesis)[D].西安:西安交通大学(Xi'an: Xi'an Jiaotong University),1991.
[4] 索南加乐(SUONAN Jia-le).同杆双回线的故障分析及继电保护,博士学位论文(Fault analysis and protective relaying of Double Circuit Lines on the Same Tower, Ph.D. Thesis)[D].西安:西安交通大学(Xi'an: Xi'an Jiaotong University),1991.
[5] 索南加乐,葛耀中(SUONAN Jia-le, GE Yao-zhong).同杆双回线跨线故障的准确定位方法(A New Accurate Fault Locating Method of the Fault between Two Lines on the Double Line on the Same Tower)[J].中国电机工程学报(Proceedings of the CSEE),1992,12(3):1-9.
[6] 葛耀中(GE Yao-zhong).新型继电保护与故障测距原理与技术(New Types of Protective Relaying and Fault Location Their Theory and Techniques)[M].西安:西安交通大学出版社(Xi'an Jiaotong University Press),1996.
[7] 董新洲,葛耀中,徐丙垠(DONG Xin-zhou, GE Yao-zhong, XU Bin-gyin).利用暂态电流行波的输电线路故障测距研究(Research of fault location based on current Travelling waves)[J].中国电机工程学报(Proceedings of the CSEE),1999,19(4):76-80.