?

本文应用一种自适应递阶遗传算法同时优化神经网络结构和连接权重进行三相桥式全控整流电路故障诊断。利用自适应递阶遗传算法同时优化神经网络结构和连接权重，很好地解决了以往利用神经网络进行故障诊断的不足，并用三相桥式全控整流电路故障诊断仿真实例证明了该方法的正确性和有效性。

1 基于改进递阶遗传算法BP网络分类器的设计
1．1 递阶遗传算法
??? K．F．Man等根据染色体中的基因结构存在递阶形式，即一些基因控制另一些基因的活动，提出了递阶遗传算法(Hierarchical GeneTIc Algorithm，HGA)。
??? 为了简要说明控制基因的活动，用整数“1”表示每一个正在激活的控制基因；用整数“0”表示每一个没有激活的控制基因。当控制基因用整数“1”标识时，表示其相连的下级结构的基因处于活动状态；当控制基因用整数“0”标识时，表示其相连的下级结构的基因处于不活动状态。这种递阶结构意味着染色体比普通遗传算法中的染色体包含的信息多，从而能够处理更为复杂的问题。因此，称编码为递阶结构染色体的遗传算法为递阶遗传算法。
??? 如图1所示，两条染色体各是由5个控制基因和5个整数表示的参数基因组成。

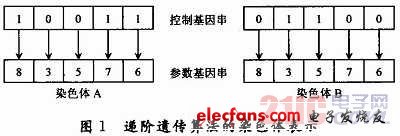
??? 其表示分别为：
????
??? 从图1可以看出，XA，XB表示染色体的长度分别为3和2，这意味着在递阶染色体结构中，虽然两条染色体的长度相同，而其表示的长度可能不同。因此，递阶遗传算法能够搜索出所有参数中适合最终目标函数的参数的长度。而且，根据具体问题，染色体可以设计为多级递阶结构，从而形成多层的染色体结构。
??? 本文采用二级递阶结构染色体描述BP网络结构和参数，其中，控制基因串表示隐节点，参数基因串表示网络的权重和相应的阈值。递阶遗传算法在操作过程中，不仅改变控制基因串的状况，而且改变参数基因串的取值。因此，训练过程中网络参数和拓扑结构可同时优化。

?

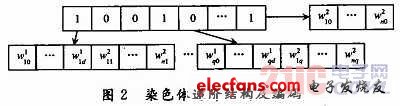
1．2 编码结构
??? 染色体递阶结构及编码如图2所示，其中，控制基因按设定的比较大的初始隐节点数(可以根据经验公式得到，其中，d为输入神经元个数，n为输出神经元个数，a为1～10之间的常数)由遗传算法随机生成0，1编码，1的个数即为有效的隐节点个数，参数基因为隐节点对应的权值及阈值，由遗传算法随机生成实数编码。另外，在参数基因串的最后附加上不受控制基因控制的输出节点的阈值参数。当达到训练代数或停止准则时，控制基因串中1的个数即为最佳隐节点个数，1所对应的参数基因串即为该隐节点对应的最优结构参数。

?