一、引言

模糊传感器是在20世纪80年代末出现的术语。随着模糊理论技术的发展，模糊传感器也得到了国内外学者们的广泛关注。模糊传感器是在经典传感器数值测量的基础上，经过模糊推理与知识集成，以自然语言符号描述的形式输出测量结果的智能传感器。一般认为，模糊传感器是以数值量为基础，能产生和处理与其相关测量的符号信息的传感器件。

二、模糊传感器的研究意义

传统的传感器是数值传感器，它将被测量映射到实数集中，以数值符号来描述被测量状态，即对被测对象给以定量的描述。这种方法既精确又严谨，还可以给出许多定量的算术表达式，但随着测量领域的不断扩大与深化，由于被测对象的多维性，被分析问题的复杂性或信息的直接获取、存储方面的困难等等原因，只进行单纯的数值测量且对测量结果以数值符号来描述，这样做有很大缺陷，例如：

（1）某些信息难以用数值符号来描述。例如在产品质量评定中，人们常用的是“优”、“次优”、“合格”、“不合格”，也可用数字1，2，3，4来描述，但数字在这里已失去通常的测量值的意义，它仅作为一个符号，不能来表征被测实体的具体特征。

（2）很多数值化的测量结果不易理解。如在测量人体血压时，人们更关注的是：老年人的血压是否正常，青年人的血压是否偏高。而实测的数据往往不能被普通人读懂，因而满足不了人们的需求。

因此，有待用新的测量理论和方法来补充。模糊传感器正是顺应人类的生活实践、生产与科学实践的需要而提出的。

三、模糊传感器的理论基础

1、符号化表示原理

模糊语言是人类表述语言的一种，因为人们对自然界事物的认识存在着一定的模糊性，用模糊符号来表述信息具有较为简单、方便，且易于进行高层逻辑推理等优点。模糊符号化表示就是利用模糊数学的理论和方法，借助于专门的技术工具，把测量得到的信息，用适合人们模糊概念的模糊语言符号加以描述的过程。符号是信息的载体，是对一个物体或事件状态的描述，它定义了实体的特征属性或实体间的关系。设Q为数值域，S为语言域，在各自的论域上有若干个元素qi、si，且表示为：

Q＝〈q1，q2，…〉 qi∈Q （1）

S＝〈s1，s2，…〉 si∈S （2）

同时，在论域Q和S上分别定义一组关系族：

R=〈R1，R2， …，Rn〉 Ri Q×Q×…×Q （3）

P=〈P1×P2×…×Pn〉 Pi S×S×…×S （4）

并且定义：D=〈Q，R〉，L=〈S，P〉

其中，D—对象关系系统，描述数值域元素及其相互关系；

L—符号关系系统，描述符号域元素及其相互关系。

设有两个映射M和F，M：Q→S，使得Si=M（qi），F:R→P，使得Pi=F（Ri）成立，且M Q×S和（qi，si） M，则称si是qi的一个符号。si的含义是qi从数值域下向语言域映射的投影，而对每一次测量qi，符号si成为qi的描述。系统原理如图1所示。

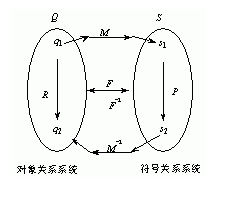
图1 符号化表示原理示意图

如果F映射是一对一映射，而M映射是同态映射，那么一定存在逆映射：F-1（Pi）＝Ri，M-1（si）＝qi。M映射可以是“单对单”或“多对单”映射。那么，在后一种情况下，符号域中的一个符号经M-1映射在数值域对应出的不是一个点，而是一个“子域”。因此，模糊符号化表示有一定的局限性，即在不同测量结构下，同一测量子集的元素对应不同的符号；或在同一测量结构下，存在测量子集的一些元素同时对应于不同的符号的情况。这一局限性可通过基于多值逻辑理论的多值符号化测量来弥补。其基本思想是：在实体测量集中，根据对实体的某一特征表现程度的不同，把测量子集Q中的元素按特征隶属度最大归类于某一子集，忽略其他特征的表现，因此只要在测量集上对实体集选取适当多个特征表示，使之与测量集中的元素相对应，就可把Q分成有限个意义相关又表现不同的子集{Qi}，对每一个Qi进行符号映射，从而实现对实体集多值符号化测量。

2、多级映射原理

虽然符号具有高级逻辑表达、易理解、人类经验与知识易集成、较宽的冗余度等特点，但与数值测量无限可分相比，符号化测量描述细节的程度和范围不够，尤其在利用符号对数值转换实现定量测量时更为突出。而多级映射原理在实现数值对符号和符号对数值转换的同时，可以扩大符号表示的细致程度和范围。

图2 多级映射原理示意图

本文概述了模糊传感器的研究意义及概念，简要介绍了模糊传感器的理论基础及实现方法，并举例说明了模糊传感器的应用。

多级映射的基本功能是实现数值→符号的变换和符号→数值变换。其原理如图2所示，它的信息传输分为两种情况：

首先是数值对符号的转换，并且是由数值域Q中的元素qi经过映射M的第一级M1映射到符号域S的子集Si，如果子集Si描述细致程度不够，则可以进行第二级映射M2，映射M2将qi映射到次子集Sij，经过若干级映射可以得到描述qi信息的符号sy；

其次，则是符号对数值的转换，由经过多级映射得到的符号sy通过映射M-1得到数字值qj。

由于自然语言表现概念的局限性，建议多级映射的级数为3级。例如，对于0℃～100℃的温度范围，每级采用7个概念，在映射级数为3级时，精度达到0.3℃。对于不需要人们直接参与的中间测量结果情况，多级映射级数可以根据需要加以确定。映射级数的多少另一方面还取决于每一级中包含概念（元素）的个数，每一级概念个数多则需要的映射级数就相应少。如果多级映射应用于包含数值输出在内的模糊传感器研究，则映射级数和传感器变换非线性误差是相关的，映射级数应该通过给定的测量不确定度加以确定。

四、模糊传感器的结构及实现方法

1、模糊传感器的结构

模糊传感器的简化结构图如图3所示。可见，模糊传感器主要由传统的数值测量单元和数值－符号转换单元组成。其核心部分就是数值－符号转换单元。但在数值－符号转换单元中进行的数值模糊化转换为符号的工作必须在专家的指导下进行。

图3 模糊传感器结构示意图

2、模糊传感器的实现方法

综上所述，要实现模糊传感器就在于寻找测量数值与模糊语言之间的变换方法，即数值的模糊化，来生成相应的语言概念。所谓语言概念生成就是要定义一个模糊语言映射作为数值域到语言域的模糊关系，从而将数值域中的数值量映射到符号域上，以实现模糊传感器的功能。这里的语言值用模糊集合来表示，模糊集合则由论域和隶属函数构成。因此模糊语言映射就是要求取相应语言概念所对应数值域上的模糊隶属函数。如何进行概念生成是实现模糊传感器的关键。目前有很多方法可以实现模糊传感器的功能。

国外很多学者对模糊传感器的实现方法进行过讨论，这里简要介绍几种：

Foulloy算法简介：模糊传感器设计的实质是模糊变换算法的设计，即参考集的选择与模糊量化。其过程是首先根据专家或熟练工人的知识和经验获取相应测量领域的一级数值/语言变换策略，然后应用模糊推理方法求取相应隶属函数。Foulloy提出了基于语义关系的概念生成方法，首先，由论域的意义来定义一个通用的概念，称属概念，使之对应数值域中论域上的主要区间，然后在此基础上定义新概念，以产生其它语义值及其意义，新概念通过语言修正器内部自动生成。Foulloy还提出了基于已知点集通过内插方法实现的模糊状态传感器，每一学习点通过Delaunay三角法在测量空间的笛卡尔积上构造模糊分割，三角法用于建立与过程状态相关的符号的模糊意义。

Benoit E等人讨论了使用符号信息时，符号语义与被测量信息在特定任务环境下的关系，认为模糊传感器必须根据测量关系来构造，并且应该可以重组以适应不同的测量关系。并提出了将基础概念作为先验信息提供给传感器，其余概念由运算自动生成的设计思想。这种方法保留了概念之间的相对语义，但不能保证与测量关系符号说明的一致性，因此必须考虑环境对测量关系的修正问题，他提出了基于定性学习以及通过复合调节说明的函数方法来进行修正。他提出了基于Delaunay多维空间的三角测量的线性插值来构造模糊分割的新方法，用以建立采用多元件测量的模糊传感器。

Stipanicer D等人认为模糊传感器是一种智能测量设备，由简单选择的传感器和推理器组成，将被测量转换为适于人类感知和理解的信号。由于知识库中存储了丰富的专家知识和经验，它可以通过简单、廉价的传感器测量相当复杂的现象。

五、模糊传感器的应用

目前，模糊传感器已被广泛应用，而且已进入平常百姓家，如模糊控制洗衣机中布量检测、水位检测、水的浑浊度检测，电饭煲中的水、饭量检测，模糊手机充电器等。另外，模糊距离传感器、模糊温度传感器、模糊色彩传感器等也是国外专家们研制的成果。随着科技的发展，科学分支的相互融合，模糊传感器也应用到了神经网络、模式识别等体系中。

六、结束语

模糊传感器的出现，不仅拓宽了经典测量学科，而且使测量科学向人类的自然语言理解方面迈出了重要的一步。模糊传感器虽然在色彩、距离等领域有一些成功的应用，但只是分散的、个别的，远未形成系统的理论体系和技术框架，实现模糊传感器的诸多关键技术尚未完全解决，还需广大测量工作者的继续探索。