近年来，基于神经网络的方法引起人们的高度重视，并被应用于传感器故障诊断领域。神经网络具有无需建立精确的数学模型，以及容错性、学习、自适应能力和非线性映射能力。因此，在空调系统故障诊断领域的应用中有较大潜力。由于小波函数具有快速衰减性，局部收敛较快等优点，本文把小波与神经网络结合起来，提出小波神经网络(WNN)的传感器故障诊断策略，用小波分析提取数据的频域特征，再使用神经网络对信号的频域特征数据做故障诊断。

　　1 小波神经网络模型

　　小波神经网络是一种以BP神经网络拓扑结构为基础，把小波基函数作为隐含层节点的传递函数，信号前向传播的同时误差反向传播的神经网络。小波神经网络模型的建立有两种：一种是用小波函数的尺度和平移参数代替神经网络隐含层的权值和阈值;另一种是将小波分析作为神经网络的前置处理，为神经网络提供输入特征向量。WNN与传统的BP神经网络结构相似，由输入层、隐含层和输出层组成，不同的是隐含层激励函数为小波基函数，其拓扑结构如图1所示。

　　

 

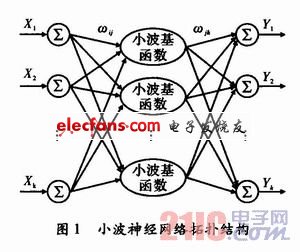
　　假设X1，X2，…，XK是小波神经网络的输入参数，Y1，Y2，…，Yk是小波神经网络的输出，ωij和ωjk为小波神经网络的权值。在输入信号为xi(i=1，2，…，k)时，隐含层的计算公式为

　　

 

　　其中，ωij为输入层与隐含层的连接权值;gj为小波基函数;g(J)为隐含层第j个节点输出值;ai为小波基函数gi的伸缩因子;bi为小波基函数gi的平移因子。

　　输出层第k个节点的总输出

　　

 

　　式中，g(i)为隐含层第i个节点输出值;ωik为隐含层与输出层的连接权值;m为输出层节点数;l为隐含层节点数。

　　小波神经网络的权值修正算法和BP神经网络权值修正算法相似，采用梯度修正算法修正网络的权值和小波基函数参数。但是，梯度下降法固有的特点使得WNN的训练过程和BP网络训练过程一样，存在着收敛速度慢、容易陷入局部极小值和容易引起振荡效应几个缺点。所以，需要对其修正算法进行改进，标准BP算法的改进主要有两种：(1)增加动量项。当误差曲面出现骤然起伏时，增加动量项可以减少振荡趋势，加快训练速度。(2)自适应调节学习速率。从误差曲面上分析，在平坦区域内学习速率η太小会使训练次数增加，因而希望增大η值，而在误差变化剧烈的区域，η太大会因调整量过大而使训练出现振荡，迭代次数增加。自适应的改变学习速率，可以减少迭代次数，提高训练速度。因此，采用采取如下方式调节学习速率，即

　　

 

　　式中，△η(t)为速率变化率;λ为学习因子;k为变量因子，一般取值在[0，1]。

　　2 传感器故障的分类

　　传感器可能发生的故障有多种，对这些故障进行分类是必要的。空调系统中传感器故障主要分为4类：偏差故障、漂移故障、精度等级降低和完全故障。前面3种称为软故障，完全故障亦为硬故障。

　　测量值和真实值之间的差异，称为测量误差。根据测量误差的性质不同，可以把测量误差分为随机误差和系统误差。系统误差主要是由于故障造成的，不同的故障类型系统误差有不同的表现形式。随机误差一般情况下服从零平均值正态分布。因此，测量值为3个值相加

　　

 

　　其中，Rt为测量变量在某一时刻的测量值;rt为测量变量在某一时刻的真实值;ut为某一时刻测量的系统误差;d为测量的随机误差。

　　2.1 完全故障

　　完全故障就是测量值不随实际值变化而变化，始终保持某一常数，即式(4)中为Rt常数。

　　2.2 偏移故障

　　偏移故障一般是指测量值与真实值之间相差某一恒定常数。由式(4)可知ut为常数。

　　2.3 漂移故障

　　漂移故障就是故障大小随时间发生线性变化的一类故障。可以表示为

　　

 

　　式中，H为漂移常数;ts和t分别指故障的起始时刻和故障发生后的某一时刻。

　　2.4 等精度降低

　　等精度降低故障和偏移、漂移故障不同，并不表现在测量的平均值出现偏差，而是测量的方差发生了相应变化。