解决几何变换的一般思路
图像几何变换又称为图像空间变换, 它将一幅图像中的坐标位置映射到另一幅图像中的新坐标位置. 我们学习几何变换的关键就是要确定这种空间映射关系, 以及映射过程中的变换参数。
几何变换不改变图像的像素值, 只是在图像平面上进行像素的重新安排。一个几何变换需要两部分运算:首先是空问变换所需的运算, 如平移、旋转和镜像等, 需要用它来表示输出图像与输入图像之间的〈像素〉映射关系:此外, 还需要使用灰度插值算法, 因为按照这种变换关系进行计算, 输出图像的像素可能被映射到输入图像的非整数坐标上。
主要有以下内容:
·图像的平移变换
·图像的镜像变换
·图像的转置变换
·图像的旋转变换
·图像的缩放
1、图像的平移变换
在进行书写matlab代码之前,先来了解一下图像平移的理论基础。设图像的高度为H,宽度为W,如下所示:
我们知道,图像是由像素组成的,而像素的集合就相当于一个二维的矩阵,每一个像素都有一个“位置”,也就是像素都有一个坐标。假设原来的像素的位置坐标为(x0,y0),经过平移量(△x,△y)后,坐标变为(x1,y1),如下所示:
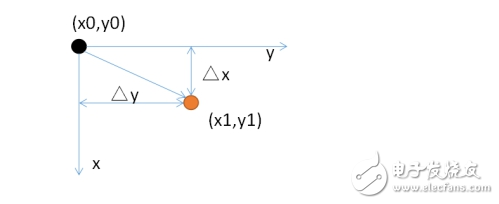
用数学式子表示可以表示为:
x1 = x0 + △x,
y1 = y0 + △y;
用矩阵表示为:
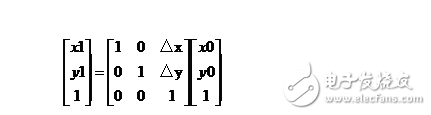
本来使用二维矩阵就可以了的,但是为了适应像素、拓展适应性,这里使用三位的向量。
式子中,矩阵:
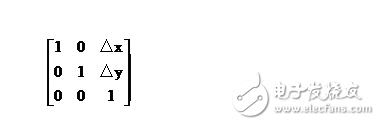
称为平移变换矩阵(因子),△x和△y为平移量。
此外,我们也知道了,图像的高度H其实也就是像素的行数,对于坐标1≤X≤H;图像的长度也就是像素的列数,对应坐标1≤Y≤W。
上面是理论基础,下面我们就用matlab实现一下图像的平移变换,相应的matlab代码如下所示:
close all ;
clear all ;
clc ;
im = imread(‘F:/图像处理/Koala.jpg’);%读入一幅图
[H,W,Z] = size(im); % 获取图像大小,H为垂直方向768点,W为水平方向1024点
I=im2double(im);%将图像类型转换成双精度
res = ones(H,W,Z); % 构造结果矩阵。每个像素点默认初始化为1(白色)
delX = 50; % 平移量X
delY = 100; % 平移量Y
tras = [1 0 delX; 0 1 delY; 0 0 1]; % 平移的变换矩阵
for x0 = 1 : H%第1行到第768行
for y0 = 1 : W%第1列到第1024列
temp = [x0; y0; 1];%将每一点的位置进行缓存,1行1列,1行2列···1行1024列
temp = tras * temp; % 根据算法进行,矩阵乘法:转换矩阵乘以原像素位置
x1 = temp(1, 1);%新的像素x1位置,也就是新的行位置(从1~768)
y1 = temp(2, 1);%新的像素y1位置,也就是新的列位置(从1~1024)
% 变换后的位置判断是否越界
if (x1 《= H) & (y1 《= W) & (x1 》= 1) & (y1 》= 1)%新的行位置要小于新的列位置
res(x1,y1,:)= I(x0,y0,:);%进行图像平移,颜色赋值
end
end
end;
set(0,‘defaultFigurePosiTIon’,[100,100,1000,500]);%设置窗口大小
set(0,‘defaultFigureColor’,[1 1 1]);%设置窗口颜色
figure;%打开一个窗口,用来显示(多幅)图像
subplot(1,2,1), imshow(I),axis on ;%显示图片,一行两列,第一幅
subplot(1,2,2), imshow(res),axis on;%显示图片,一行两列,第二幅
我们先来看一下效果,然后着重分析一下代码,效果如下所示:
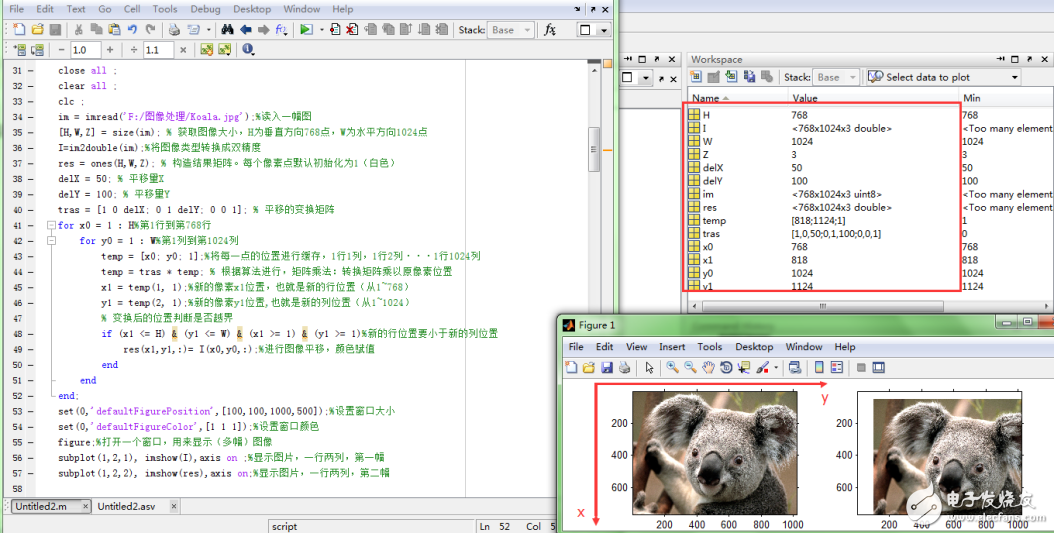
然后下面我们分析一下关键的代码:
读入图像之后,得到im,我们可以看到im是一个三维的变量,包括了像素的位置(高度(即垂直长度)和宽度(即水平长度)),像素的颜色。(注,24位真彩图:也是用矩阵表示,图像像素直接用RGB颜色显示,而不是通过颜色索引表。图像像素的颜色用三个变量表示即(R,G,B),每个变量从0~255变化,因此一个像素也就是8bit*3=24bit,一个像素用24bit表示可以有2^24种颜色。)我们可以看到会有unit8,就是8bit的原因。
然后我们获取图像的大小,用H,W,Z三个变量接收,其中H接收了图片的高度(也就是垂直长度),W接收了图片的宽度(水平长度),然后Z接收了图片的颜色值。
然后我们将图像转换成双精度类型I,这是因为使用双精度可以仿真在转换过程中发生精度损失的问题,也是方便我们进行转换。转换之后,我们可以看到unit8的类型别我们转换成了double类型。
接着,我们构造一个图像res矩阵,这个图像首先进行归一化,也就是让里面的元素全部为1,对于图像,就是一张白色的图片了。这个图像主要是用来“保存”我们进行位移后的图像。
然后我们就设置平移量、构造平移变换矩阵。这个矩阵我们根据前面的理论部分可以得到。
接着便是重点了,进行平移变换。我们来一句一句解读这个循环。当x0=1,y0=1时,得到第一个像素的位置,也就是(x0,y0)这个像素,然后将这个像素位置进行缓存,也就是构造一个矩阵temp,即理论中的:

然后进行位置转换,也就是进行矩阵相乘,用变换矩阵乘以原像素矩阵,得到了变换后像素矩阵:

接着,我们需要把变换后的像素位置“提取”出来,用x1,y1进行存储;为什么要获取位置呢?这是因为我们要判断这个像素是否越界了,也就是进行平移之后,得到的这个像素位置是否还存在显示区域里面,也就是我们的
if (x 《= H) & (y 《= W) & (x 》= 1) & (y 》= 1) 语句
当还在显示区域里面时,我们要进行移位显示:
res(x1,y1,:)= I(x0,y0,:);%进行图像平移,颜色赋值
这个语句的含义是,把I中的RGB值(也就是颜色值)赋值给res,也就是说,前面矩阵相乘只是移动的像素位置,但是颜色没有进行移动,这里进行图像颜色的平移,当x0=1,y0=1时,把该点的位置图像颜色进行移动过去。
当x0=1,y0=2时,移动第二点。我们可以看到,这里的代码是:从左到右平移,也就是先进行宽度的平移;从上到下,进行高度的平移。当两个循环完成之后,图像也就像平移完成了。
最后的代码就是显示图像了,其中axis on 的意思是打开左边,方便我们进行查看平移后的位置。从上面的效果我们可以得到,delx表示的高度的平移量,delx为正值时往下平移,delx为负值时往上平移;而dely表示的宽度的平移量,正值往右平移,负值往左平移。