基于电压型变频调速系统滤波参数的计算
0 引 言
在电压型变频调速系统中,滤波电容参数CF的计算和正确选择对于保证系统的调节质量及降低设计成本具有重要而现实的意义。滤波电容参数过大或过小,不只是影响系统工作的稳定性,而且电路中的高频信号会严重影响信号和通信系统,也可能导致接至同一电网上的另外一些系统误动作。
因此,直流环节滤波器在变频器供电的传动系统中是一个相当重要的功能器件,必须正确合理的选择。但在实际的传动系统设计中,工程人员大多基于经验公式,而不是根据引入逆变器开关策略和负荷特性进行计算,这就难于大范围改变逆变器的开关频率、脉宽。因此,存在较大的局限性。
在此从电压型变频调速系统的基本原理出发,引入逆变器的开关策略,导出电容CF在工作过程中充放电电流的变化规律,经简化近似,求得了充电过程中电容上电荷量的最大值,从而得到确定电容参数的工程计算公式,该公式简单,物理概念清楚,便于在工程实际中应用。
1 电压型变频调速系统的构成及工作原理
电压型变频调速系统的原理图如图1所示。
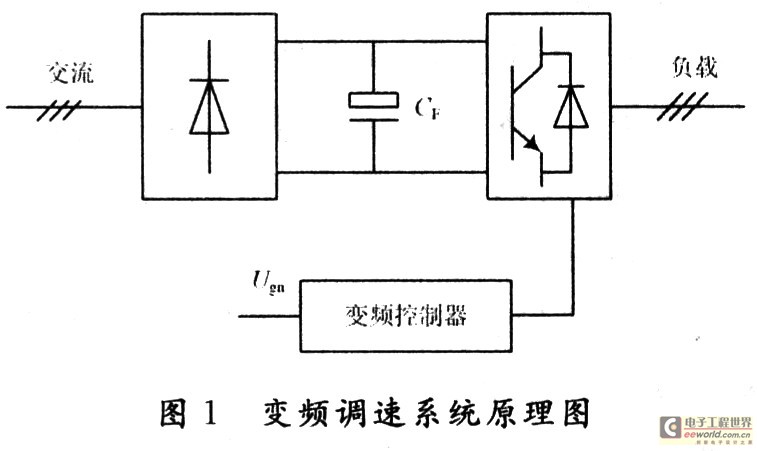
由图1可见,三相交流电经桥式整流转变成直流电,再经电容CF滤波,施加到由GTR1-GTR6组成的逆变桥逆变成电压和频率可调的三相交流电,供给三相异步电动机。其电压和频率的协调控制由变频控制器实现。
该系统滤波电容的作用是:
(1)起滤波作用,用来限制逆变器输入端电压的脉动;
(2)当异步电动机运行于再生制动状态时,吸收经逆变桥回送到直流环节的电能。
很显然,该系统的直流滤波环节就是滤波电容CF。该系统滤波参数的计算就归结为电容参数CF的计算。
2 直流环节的等效电路及充放电电流的计算
基于如下几个方面的考虑:
(1)逆变器在工作过程中,电容两端电压的峰-峰值应当小于指标规定的数值;
(2)直流环节的损耗应保持在最小值;
(3)逆变器和感应电动机中产生的瞬变现象应充分得到阻尼;
(4)直流环节的参数应不影响整个系统的稳定性。
于是可得到直流环节的等效电路如图二所示。
由图2电路图,设电流i1(t)纹波很小,则:
i1(t)=Id
于是可得到:
![]()
式中:iC(t)是流经CF的电流;Id为直流电源所提供的电流;i2(t)为去逆变器的电流。
设逆变器为六阶梯波逆变器,并且把逆变器当作开关来模拟。在忽略异步电动机旋转电势和异步电动机激磁电流影响的情况下,可得变频电机的静止模型和等效电路如图3所示。

图3中L1为每相定子绕组的漏感值;L2为每相转子绕组漏感折算到定子侧的数值;R1为每相定子绕组的电阻值;R2为每相转子绕组电阻值折算到定子侧值。这样当逆变器正常工作时(即S合上),根据基尔霍夫电压定律可得:
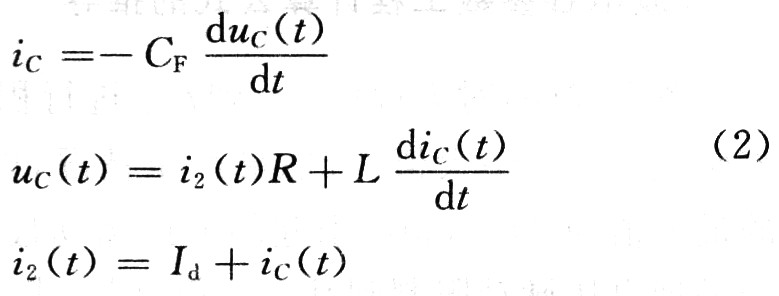
其初始条件为:UC(0)=(1+K/2)Ud,iC(0)=0,i2(0)=0。式中K为纹波系数。
由方程(2)可得:
![]()
其齐次方程的特征方程为:
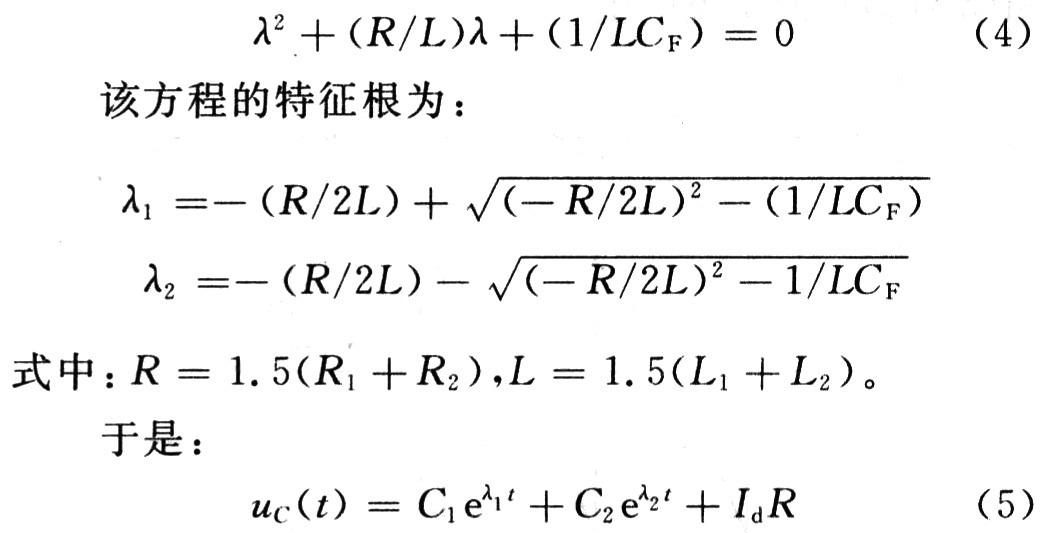
式中:C1和C2是由初始条件所确定的常数。当t=0(即逆变器开始工作)时:

式(7)和式(8)分别为电容两端电压和电容放电时电流的变化规律。
同理可求得电容两端在充电过程中C两端电压的变化规律,在此略去。于是可得到uC(t),iC(t),i2(t)的波形图如图4所示。

3 滤波电容参数工程计算公式的推导
考虑式(8)对iC(t)从TI到TI+1。进行积分,可得到电容所充电荷的最大值。考虑最严重情况,电容存储电荷的最大值为△QM,相应引起的电压脉动最大值为△UP。于是把电压脉动限制到某一定值,则要求:
CF=△QM/△UP (9)
式(9)即为六阶梯波逆变器滤波电容参数的计算公式。对所研究的系统来说,逆变器为SPWM逆变器,它和六阶梯波逆变器的差别就是开关的频率不同,也即就是电容充放电的时间不同,而且通过逆变器输出的是SPWM波形的交流电压。
考虑到在1个充放电周期内,电容所充电荷等于放电电荷。设放电时间为T,则有:

又根据电容两端电压脉动系数(按照峰一峰值定义)

考虑到对中小功率电机来说,R较小,可以忽略。于是式(12)可简化为:
![]()
式(13)表明:
(1)系统要求的电压脉动越小,则所需滤波电容量越大;
(2)变频调压的频率越高,则要求CF的容量可以减小;
(3)电机每相漏感L越大,则要求CF的容量可以减小。
综上所述,滤波电容参数计算应考虑最严重情况为宜。其漏波电容的电压额定值按Ucc≥1.5Ud选取即可。
4 结 语
上述设计思想在实验室JR2-4S 3 kW异步电机变频调速系统中进行了实验。实验电机的参数为:Ule=380 V,Ile=6.9 V,E2e=195 V,I2e=9.5 A,ne=1 400 rpm,λM=2。在要求电压脉动系数K=0.02的情况下,理论计算参数CF=650μF,而系统实际参数CF=600μF,两者基本吻合。实验结果表明其设计思想基本正确。这里所推荐的工程计算公式可用于中小功率变频调速系统滤波电容参数的计算。