|
基于SEPIC的功率因数校正电路的参数设计与分析
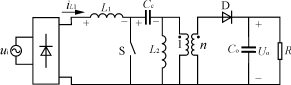
1 引言 电力电子装置日益广泛的应用，使得谐波污染问题引起了人们越来越多的关注。电力电子技术的进步，使得功率因数校正问题的研究也越来越深入。传统的功率因数校正电路由Boost电路构成。这种电路控制复杂，输出电压比输入高，难以实现输入输出的电气隔离。而由反激电路构成的功率因数校正电路必须工作在电感电流断续的状态，往往需要大体积的EMI滤波器。而SEPIC电路用于PFC有着其天然优势。由于其前级类似于Boost，从而可以保证输入电流的连续，减小了输入EMI；而其输出又类似于反激，易于实现电气隔离。近来，SEPIC-PFC电路正受到越来越多的关注。[1][2][3][4] 单独的SEPIC电路只须工作在电流断续状态就能自然实现PFC，这里所说的断续是指二极管上的电流断续，而输入升压电感上的电流是连续的。在开环工作状态下其理论功率因数为1，因此，无需专用控制芯片[2]。 2 SEPIC-PFC电路的工作原理 SEPIC-PFC电路原理如图1所示，输入交流电压ui=Uisinωt。假设开关频率比母线频率大得多，由“准稳态”的分析方法及SEPIC电路的工作原理[6]可以知道：电容Cc上的电压ucc=Ui|sinωt|。
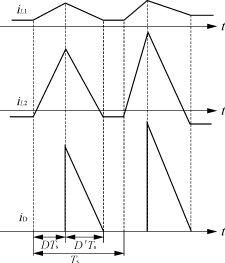
图1 SEPIC-PFC电路 在一个开关周期内，电路工作可以分为三个模态[2]。 2.1 工作模态1 S开通，电路模态如图2（a）所示，假定电路工作在二极管电流断续，L1电流连续的状态。S开通前有 iL1=－iL2=i1当ton=DTs，S导通结束时，如图2（d）所示，应有 iL1,pk=i1＋ iL2,pk=－i1＋ 式中：D为占空比； ui=Ui|sinωt|； Ts为开关周期； i1，－i1，iL1,pk，iL2,pk分别为S开通前L1，L2上的电流及此模态结束时L1，L2上的电流。 2.2 工作模态2 S关断，D导通，电路模态如图2（b）所示，此时，L1，L2同时向副边传输能量，Cc充电。S关断瞬间，二极管上电流最大值为 iD,pk= 式中：n为变压器副边与原边匝数之比； Leq= 模态2结束时应有 iL1=i1＋ iL2=－i1＋ 式中：D′Ts为该模态持续时间。 显然，当 D′Ts= 式中：M=Uo/Ui。
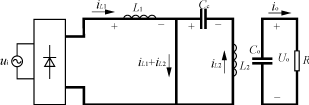
（a） 电路模态1等效电路
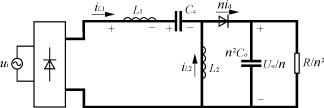
（b） 电路模态2等效电路
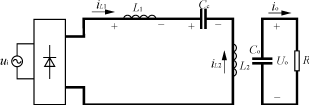
（c） 电路模态3等效电路
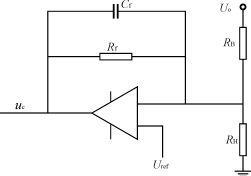
（d） iL1，iL2，iD电流示意图 图2 电路三个工作模态等效电路与相关电流示意图 2.3 工作模态3 S关断，D关断，电路模态如图2（c）所示，此时，L1，L2上的电流分别为i1，－i1。 如图2（d）所示，二极管上的电流iD在一个开关周期的平均值为 iD,avg= 将式（3），式（6）代入可得 iD,avg= iD在一个母线周期内的平均值为 ID,avg= 由于在一个开关周期内，L1，L2，Cc并不吸收能量， 因此有 uiiin=UoiD,avg从而输入电流在一个开关周期内的平均值iin为 iin= 式中：I1= 因此，iin在理论上是一个与ui同相位的正弦量。 3 输出电压二倍线频纹波 与很多PFC预调节器一样，SEPIC-PFC电路的输出存在二倍线频的纹波电压。由式（7），式（8）可以得到 iD,avg=ID,avg－ID,avgcos(2ωt) 可导出二倍线频纹波电压Δv为 Δv= 4 占空比对于输入电流谐波的影响 由式（9）可知，如果占空比固定，则输入电流是一个理想的正弦量。由于实际稳压需要，往往要加上电压环，对占空比进行调节。设D=D＋ΔD，假定ΔD《D，则应有 D2≈D2＋2DΔD=D2＋ 则iin=I1|sinωt|＋2ΔI1|sinωt| (11) 式中：D，ΔD，Δ分别为D的平均值，D的变化量，D的相对变化量； I1为I1的直流分量。 显然，如果Δ是个时变的量，输入电流就会出现畸变，只要占空比的相对变化量是一定的，其输入电流畸变就是一定的。因此，为了保证输入电流THD的要求，ΔD/D应控制在一定的范围内。 5 SEPIC-PFC电路的主要参数设计原则 5.1 等效电感Leq设计原则 要保证输入电流的正弦性和与ui的同相位性，必须让电路工作在二极管电流断续和恒占空比状态，因此有 t=DTs＋D′Ts<Ts 即 DTs＋ 可以得到 D(1＋ 考虑最恶劣的条件|sinωt|=1则应有 D< 由式（8）可解得D= Leq< 5.2 D与n的设计原则 由D< 由式（3）可知，在半个线周期内iD,pk,max= 要使n有值，必须满足 M 这样，可以解得：1－D> ID,max> 显然，占空比越大，二极管上的峰值电流就越大，并且D>0，则ID,max必须大于4倍的输出平均电流。这里与变压器匝比无关。不管如何设计，只要工作在断续状态，二极管上的峰值电流就一定大于4倍的输出平均电流。 在给定ID,max的情况下又有 D<1－ 5.3 控制电路参数设计原则 虽然PFC电路的工作方式与普通DC/DC变换器一样，但对于控制电路的设计，却有本质上的区别。一般DC/DC补偿器原则是提高稳定性和抑制开关噪声，而PFC的主要目的在于抑制二倍线频的电压纹波[2]。 为了满足THD的要求，输出电压纹波对补偿器的输出的影响应在一定的范围中[5]，即 GΔU<Δu （15） 式中：G为补偿器在二倍线频处的增益； ΔU为电压纹波； u为补偿器输出值的直流分量。 由此可以确定电压补偿器的参数范围。如采用图3所示电压补偿器，应有 G(j2ω)=
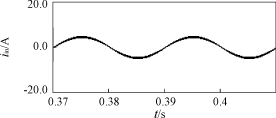
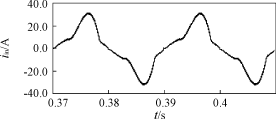
图3 电压补偿器 若2ωRfCf>>1，则有 |G(j2ω)|= 6 实例设计及仿真分析 根据以上分析，以220V，50Hz输入，48V，500W输出，50kHz开关频率为背景设计SEPIC-PFC电路，控制电路采用图3所示电压补偿器，占空比相对变化量控制在2％。滤波电容为10000μF，L1可根据输入电流纹波条件进行选取，Cc可根据式（18）进行选取[5]。 (5％～10％)ωs= 图4(a)为D=0.5时，按上述原则设计的主电路参数所得到的开环输入电流波形，图4(b)为相同主电路参数D=0.8时的开环输入电流波形，由于D=0.8时电路已不满足断续条件，输入电流畸变明显变大。
(a) D=0.5
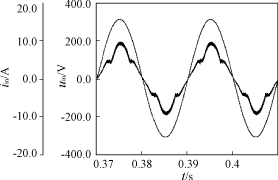
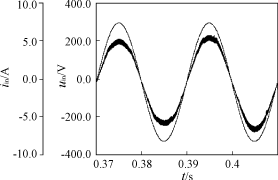
(b) D=0.8 图4 不同占空比下的开环输入电流波形 表1，表2，表3为在不同的占空比下的电路仿真数据。由这组数据可以看出，在同一额定占空比的情况下，THD随着负载的减小而减小，由于占空比的变化率受到控制，相同负载不同额定占空比情况下THD变化不大。随着占空比的增大，输出电压负载调整率在减小，电路稳压能力提高，这与理论分析一致。图5,图6分别为额定工作占空比为0.5，满载和1/3负载时的输入电压、电流波形，其中幅值较大的为输入电压，较小的为输入电流。 表1 D=0.2的仿真数据
Cc=0.51μF Cf=2.3μF Rf=6.9kΩ 表2 D=0.3的仿真数据
Cc=0.4μF Cf=1.4μF Rf=11.4kΩ 表3 D=0.5的仿真数据
Cc=0.2μF Cf=1μF Rf=16kΩ
图5 满载时输入电压电流波形
图6 1/3载时输入电压电流波形 7 结语 SEPIC电路只要工作在断续状态就能做到单位功率因数校正。占空比的相对变化量越大，THD就越大。只须控制占空比的相对变化量就可以控制输入电流的THD。占空比的直流分量越大，输出电压的负载调整率就越小。 |
DTs （1）
DTs （2）
=
（3）
。
DTs－
D′Ts （4）
DTs－
D′Ts （5）
DTs=
D′Ts时该模态结束，可以得出该模态持续时间为
|sinωt| （6）
（7）
=
（8）
iD,avg=
|sinωt|=I1|sinωt| （9）
。
(10)
=D2＋2D2Δ
|sinωt|<Ts
|sinωt|)<1
（12）
代入式（12）可得
（13）
可知，若D与M都是已知的，可得n<M
，这样，满足电路断续的条件关键在于变压器匝比n的选择。如果n选择过大，则D必须很小，由式（13）知Leq会很小，一般L1》L2，Leq≈L2，这样，L2上的电流脉动就会很大，如果n选择过小，L2上的电流脉动会减小，由式（3）可知iD,pk会很大。因此，n的选取将对电路器件应力有着很大影响。
给定iD,pk,max<ID,max，其中iD,pk,max为二极管电流最大值，ID,max为二极管允许电流最大值。一般，由L1》L2可知id,pk,max≈
。因此，只须
<ID,max。考虑n<M
，可综合解得n的范围为
<n<M
>
，将式（8）代入可得
（14）
（16）
（17）
（18）
