基于重复控制的全数字UPS逆变器

您现在的位置是：首页 > 电源

基于重复控制的全数字UPS逆变器

2020-07-31 09:05:30

基于重复控制的全数字UPS逆变器

摘要：分析了逆变器波形重复控制技术的原理和设计方法，提出了双环PI控制和重复控制相结合的复合控制方法，仿真和实验结果表明该方法对于非线性负载下的UPS逆变器输出波形具有校正作用。

关键词：重复控制；UPS逆变器；双环PI控制

1 引言

衡量UPS逆变器性能的好坏，通常有以下一些指标：电压、频率、总谐波含量（THD）、负载调整率、动态响应等，上述这些指标的好坏是与逆变器的控制息息相关的。由于电力电子设备的模拟控制技术存在着一些其自身无法克服的缺点^[1]，控制手段已经大大落后于现代控制理论的发展，所以其向数字控制的转变已是必然趋势。

UPS的应用场合要求非常高，因此，单电压环控制显然无法满足应用要求，为了提高逆变器的静态动态特性，需要采用多环控制技术。电流模式控制是一种多环控制策略，它用误差电压的调节输出作为反馈电流的指令，能够获得比较好的静态动态特性,但是不能解决在非线性负载（如整流桥负载）下输出电压THD较高的问题。近年来，随着电机控制的专用DSP的推出，基于DSP的逆变器数字控制技术发展很快，应用波形重复控制技术^[4，5]，可以有效地解决上面提到的问题。但是重复控制也有缺点，就是其动态特性非常差。本文介绍的复合控制把上述两种控制方法结合在一起，扬长避短，获得了很好的效果。

2 电感电流模式控制

一般有以下几种电流模式控制方法^[3]：滞环电流控制，电流预测控制和SPWM电流控制。其中SPWM电流控制方法是将电流误差信号与三角波比较，产生4路SPWM控制信号，它的开关频率是恒定的，同时控制逻辑也很容易实现。SPWM电流控制在电感电流模式控制中是一种比较好的控制方法。图1是电感电流模式控制框图，参考正弦电压与输出电压相减后得到误差电压，误差电压经过PI调节之后的输出作为电感电流的指令，电流误差信号经过比例调节之后与三角波比较产生控制信号。由于电感电流等于电容电流与负载电流之和，其中电容电流为输出电压的微分，电感电流模式控制相当于使系统能超前对输出电压进行控制，因此能够取得比较好的动态特性。另外电感电流中包含了负载电流，所以又可以起到对负载限流的作用。

图1 电感电流模式双环控制

3 重复控制

重复控制是一种基于内模原理的控制方法[4]，内模原理指出：系统在稳定状态下无稳态误差地跟踪参考输入信号的前提条件是闭环控制系统稳定且闭环控制系统中包含有参考输入信号的传递函数。

为了实现重复控制系统，必须首先产生一个周期性的激励信号来消除由参考输入信号或干扰产生的周期性误差。图2是产生这个周期性激励信号的两种方法。

(a)方法1

(b)方法2

图2重复控制器中的内模原理

图2（a）中的周期激励信号由模拟的方法实现，图2（b）中的周期激励信号由数字的方法实现。图2（b）中的N为每个工频周期内输出电压的采样次数，满足关系式：

L=NT_s（1）

式中：T_s为输出电压的采样周期。

输入信号E对应的是逆变器控制中的输出电压的误差信号，图中的内模结构是一个正反馈系统，输出C是对E的逐周期累加，只要输入不为零，输出就将逐周期变化，直至系统的输出电压跟踪误差为零。这时，输出C将保持不变，从而使系统的输出电压一直能够无误差的跟踪输入参考信号。

逆变器的重复控制结构框图[4]如图3所示，虚线框内即为离散重复控制器，各环节的传递函数介绍如下：

图3逆变器重复控制结构框图

1）z^－N：周期延时环节，延时一个基波周期（工频周期），使周期误差从下一个周期开始校正，同时使超前环节的设置成为可能。

2）Q(z)：为克服对象模型不精确，增强系统的稳定性而设置的低通滤波器或小于1的常数。

3）S(z)：补偿器，用于修正SPWM逆变器模型的幅频特性曲线，使之适合重复控制的要求。

4）z^K：时间超前环节，补偿由于S(z)和SPWM逆变器产生的时间延迟。

5）K_r：重复控制器的增益，决定了重复控制器的输出U_r的幅度，同时K_r的取值直接影响了重复控制器的稳定性，一般取一个小于1的常数，以保证系统的稳定。

6）P(z)：SPWM逆变器的简化离散数学模型。

令：

H(z)=Q(z)－P(z)K_rS(z)z^k(2)

对应于频域的表达式为：

H(e^jωTs)=Q(e^jωTs)－e^jωkTsK_rS(e^jωTs)P(e^jωTs) (3)

很明显，闭环系统稳定的充要条件是^[4]：

|H(e^jωTs)|<1 (4)

Q(e^jωTs)通常是一个接近于1的常数，或者是一个低通滤波器。在重复控制器的作用下，逆变器的输出电压的谐波幅度由下式决定：

|e(e^jωTs)|=|r(e^jωTs)|＋|d(e^jωTs)| （5）

从上式可以看出，稳定状态下，参考跟踪误差|r(e^jωTs)|和重复控制中的周期性扰动误差|d(e^jωTs)|被衰减到原来的倍。因此，反映了重复控制系统的谐波抑制能力，定义它为谐波抑制因子。

4 重复控制器的设计

重复控制器的设计首先要保证系统的稳定性，然后才是考虑如何减小系统的稳态误差，抑制逆变器输出电压的谐波^[5]。在UPS系统中，输出电压的谐波主要集中在中低频段，因此在进行重复控制器的设计时，只考虑中低频段系统的谐波抑制，在系统的稳定性分析时兼顾高频段即可。下面给出了一种重复控制器的设计方法：

1）确定周期延时系数N

输出电压的采样周期为T_s，则一个周期内的采样次数即延时系数N=T/T_s。

2）逆变器的简化离散数学模型P(z)

逆变器的数学模型可以有两种方法，第一种是实验的方法^[5]描出逆变器的幅频特性曲线，通过软件拟合后得到模型。另一种是忽略开关器件，只考虑LC滤波器和寄生电阻的二阶模型。

3）补偿环节Q(z)

前面已经提到，Q(z)通常是一个接近于1的常数，或者是一个低通滤波器，设计中取Q(z)=0.95。

4）逆变器模型幅频特性补偿器S(z)

S(z)实际上是由S₁(z)和S₂(z)复合而成的。由于逆变器的LC滤波器在谐振频率点上增益很大（如果没有阻尼，则为无穷大），通过S(z)的补偿，希望频率从0到谐振点的增益接近于0dB，通过谐振点之后，增益大大减小。S₁(z)通常采用梳状滤波器，这样没有相位延迟。S₂(z)通常采用一个剪切频率等于LC谐振频率的二阶低通滤波器，通常可借助MATLAB进行设计。

5 复合控制方法

UPS逆变器采用重复控制技术，在线性和非线性负载下均可以获得良好的静态特性，但是由于重复控制延时1个工频周期的控制特点，使得单独使用重复控制的UPS逆变器动态特性极差，基本上无法满足UPS逆变器的各项指标，因此本文提出了双环PI控制和重复控制相结合的复合控制方法。图4是这种复合控制方法的结构框图。图中左上角虚线框内的控制器为离散重复控制器，主要用来消除输出电压周期性的跟踪误差，减小UPS逆变器在整流桥负载下的输出电压畸变。双环PI控制器主要是对输出电压跟踪误差进行实时的控制，减小不确定的干扰造成的输出电压畸变。

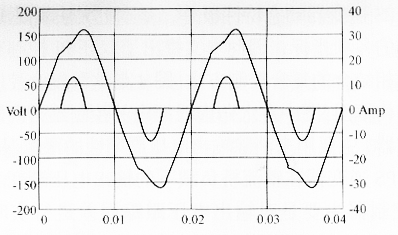
图4 双环PI和重复控制的复合控制框图

上述复合控制的结构实际上是一种并联的结构，重复控制器的输入为电压误差信号，输出为电压控制信号；双环PI控制器的输入为电压误差信号和电感电流信号，双环控制器的输出和重复控制器的输出相加之后再输入比较器，产生逆变桥的门极脉冲。两种控制方法的结合，一方面，当系统处在稳态时，重复控制器起主要的调节作用，使得稳态下输出电压能很好地跟踪参考正弦波。另一方面，当系统出现比较大的瞬态干扰时，双环PI控制会起到比较大的作用，调节输出电压，使跟踪误差迅速减小。

图5为MATLAB的SIMULINK工具箱下的仿真结果，图5（a）为双环控制，图5（b）复合控制。可以很明显得看到，采用复合控制的UPS逆变器的输出波形的畸变已经变得很小。