配电网络重构的改进混合遗传算法

本文提出一种基于改进的混合遗传算法的配电网重构算法，在算法中使用可操作开关支路的整数编号的排列顺序来表示染色体，并通过译码器的设计来映射染色体所对应的辐射状网络结构，避免了产生不可行解的情况，大大提高了算法的运算效率。同时在算法中引入了局部寻优算子，改善了算法的局部寻优性能。算例结果表明本算法是高效，可行的。
　　关健字 网络重构；遗传算法；局部寻优算法

A refined hybrid geneTIc algorithm for
distribuTIon network reconfiguraTIon

ZHENG Xin1，YANG Li-xi1，C.T.Tse2

(1.College of Electrical Engineering，ZhengZhou University，
ZhengZhou，450002，China；
2.The Hong Kong Polytechnic University，Electric Engineering 
Department，China)

　　Abstract: This paper proposes an improved soluTIon for distribution network reconfiguration based on a refined hybrid genetic algorithm. In the algorithm the "the integer permutation" encoding is adopted with each integer representing one controllable switch. A decoder is designed to decide the final network configuration corresponding every chromosome. A local search operator is combined with the genetic algorithm which improve the local optimal capability of the algorithm. The computational result on a tested system demonstrate the algorithm is feasible and efficient. 
　　Key words: Network reconfiguration；Hybrid genetic algorithm；Local search algorithm；

1 引言
　　基于网损最小的配网重构问题是一个典型的非线性、多约束的整数组合优化问题，配电网的辐射状结构和弱环网特性是其重构的前提条件。基于图论，配电网的结构可以用图G(N,B)描述，N表示电源节点和负荷节点的集合，B表示馈线段集合，配网的辐射状结构就由图的多个树来组成，T={t1t2t3t4...tn,l1l2...lm}，其中树支t为供电支路，连支l为联络支路。这样，配网重构问题，可以被描述为在图中寻找一个使得总网损最小并满足运行约束的树状结构。一个大型的配网包含众多的节点和支路，因此图中支撑树的组合数目极大，若穷举所有的树，算法将非常的低效。
　　遗传算法具有全局收敛性、无可微性要求、具有很好的鲁棒性等优点，特别适合于求解组合优化问题。另外，与一般的随机搜索方法进行的盲目无向搜索不同，遗传算法进行的是高效有向的全局搜索，能够逐步地逼近并收敛于全局最优解。因此，遗传算法在配网重构中得到越来越广泛的应用。
　　但是，遗传算法对于求解配网重构这样的非线性组合优化问题，还存在两个重要的缺陷，一是父代的优质基因结构对于子代影响甚小，采用常规遗传算法，收敛速度相当慢；二是配网重构是一个强约束的问题，对于电流、电压等约束，可以用惩罚因子来进行约束，但对于出现环网和孤岛的组合无法用一个合适的评价函数来进行评价。文献[1]-[4]提出了不同编码、杂交和变异算子设计方法虽然在一定程度上提高了算法的效率，但是这些基于二进制编码方法的算法在产生下一代的时候都不可避免地出现大量的不可行解。在这些文献中对于不可行解的处理方法分为两种，一种是删除，补充可行解进入新生代；另一种方法是修补，将不可行解的网络结构通过打开开关解环，合上开关消除孤岛，使不可行解变为可行解。这两种方法虽然在理论上是可行的，但只适合于每一代出现很少量的不可行解的情况。在一个复杂、多环的配网中，这些算法在每一代中都将产生大量的不可行解，要耗费大量的时间来判断解是否可行，而补充新的可行解与修补不可行解也是非常困难和耗时的，增加了算法的复杂度。同时由于进行大量的修补和补充新个体，子代不能保持与父代的亲体相似性，父代中的优质基因结构在子代中遭到完全破坏，算法最终可能蜕变成盲目的随机搜索，收敛速度慢，甚至出现不能收敛的现象，失去了遗传算法的意义。
　　本文提出一种改进的混合遗传算法，在常规的遗传算法中加入局部寻优算子来改善算法的局部寻优性能，同时通过编码器和译码器相结合的设计方法完全避免了出现不可行解的问题，进一步提高了遗传算法的搜索效率，从而加快遗传算法的收敛速度。

2　配网重构的数学模型
　　配网重构的目的就是在满足运行约束的前提下，使系统的网损达到最小。因此配网重构的目标函数可以表示为：
 
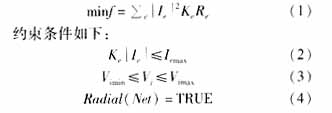
其中:Ie是支路e的电流，Re是支路e的电阻，Ke表示支路的开关状态，1表示支路开关处于闭合状态，0表示支路开关处于断开状态；(2)式代表支路电流过载约束，Iemax表示支路电流的上限；（3）式代表节点电压约束，Vimin、Vimax分别表示节点的电压的上下限，（4）式代表辐射状网络且不出现孤岛的拓扑约束。本文通过前推回代的潮流算法来求解配网网损，并用约束条件进行验证。

3　遗传算法在网络重构中的改进
3. 1 编码和译码策略
    编码设计就是如何用一个染色体来表示一个唯一的配电网网络结构；本文将配电网中所有的可操作的开关支路进行整数编号，染色体是由所有这些支路号的随意排列组成，染色体中不允许出现相同的支路号，染色体的长度为可操作开关支路的数目。如一个16节点的配电系统，16条支路从1到16进行编号，其中一个染色体就可以表示为：
    [1 2 3 5 6 7 8 9 10 12 14 15 16 4 11 13]
    对于遗传算法而言，仅随机产生不同顺序的串，为了使串表示一个有效的网络拓扑，这就需借助于译码器的实现。译码器的目标就是如何根据染色体的编码来构造出一个唯一的支撑树。
    本文在译码器的设计中，采取避圈法生成树的构造方法：图开始时，只有节点没有边，树支和连支的集合为空，按照染色体中支路号从左到右的排列顺序，选择支路号对应的一条边来加入图中；如果与图中的边不构成环，就作为树支放入树支集合中，否则作为连支放入连支集合中，重复这个过程，直到不能进行为止；这样最后将形成树的形式，树支即为闭合支路，连支为打开的联络支路。可见在避圈法生成树的过程中，在一个弱环中先加入的边会成为树支，而最后加入的边由于会形成环，只能作为连支，所以加入边的顺序不同也就是染色体的不同产生的树就有可能不同，同时通过这种方法每一个染色体必然只对应出唯一一个树状结构的配网。虽然不同的染色体对应的树可能是一样的，如在上面的树如果表示为一个染色体，随意改变中树支的排列顺序和随意改变连支的排列顺序根据避圈法生成的树都是一样的，但是我们可以在产生初始代时通过连续大范围的交叉转换来减少出现等价染色体的机率。在本文的算例中，通过特定的交叉和变异方法在每一代中只有很少的机率出现等价或相同的染色体。由于这种通过译码器构造支撑树的方法，对应的很自然的就是可行解，所以就不需要再判断网络结构是否符合网络拓扑约束的问题，省去了各种对不可行解的处理步骤，大大提高了解的质量和算法的运算效率，加快了解的收敛速度。
3.2 交叉算子设计
    基于构造支撑树的顺序编码，若采用简单的一点或多点交叉策略，必然以极大的概率产生不可行的染色体，因此本文采用与部分匹配交叉比较类似的交叉方法，方法如下：
    (1)随机在串中选择一个交配区域，如两父串及交配区域选定为:
    A=12|3456|789     B=98|7654|321
    (2)将B的交配区域加到A的前面或后面，A的交配区域加到B前面或后面得到:
    A′=7654|123456789     B′=3456|987654321
    (3)在A′和B′中自交配区域后依次删除与交配区相同的城市码、得到最终的两子串为:
    A″=765412389   B″=345698721
    与其它方法相比，这种方法在两父类相同的情况下仍能产生一定程度的变异效果，这对维持群体内一定的多样化特性有一定的作用，实验中也显示了较好的结果。
3.3 变异
　　为了维持群体内的多样化，本文采用随机连续多次对换的变异技术，使可行解在顺序上有了较大的变化，以抑制交叉中有可能产生的同化作用。
　　所谓随机对换变异，就是随机选择串中的两点，交换其编码。例如对于串A:
      A=12|3456|789
　　如果随机产生的交换点是2和7，则串A中的第2点和第7点将对换，对换后，串A变为：
     A′=17|3456|289
　　由于经过一次对换后，A′仍然有可能与A表示为同一个网络结构，所以本文采取连续多次的对换操作，来增强变异的效果。
3.4 更新
　　本文采用代间更新的方式，由代沟G控制每一代群体中个体被更新的百分比，在t代N个个体中有(1-G).N个适应度最高的个体被选择完全复制到t+1代中去，即每代只产生N*G个新个体。代间更新的方式为遗传算法利用优化过程中的历史信息提供了条件，加快了遗传算法的收敛过程，但当代沟过小时，可能会造成遗传算法的过早收敛，G一般取0. 3～1，本文取0. 8。
3.5 适应度函数
    由于遗传算法是一种在给定的解空间内不受约束的随机搜索算法，因此必须构造一个精确的适应度函数指导遗传算法的搜索方向向着最优解逼近。本文中适应度函数由目标函数和惩罚函数组成，定义如下：
 
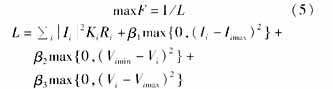
其中:B1、B2、B3是惩罚因子，通常取较大的数，以加大惩罚力度。
    计算个体的适应度，需要用译码器对个体进行解码，求出其对应的网络结构，然后调用潮流计算程序计算出节点电压和支路电流代入公式（5）即计算出个体的适应度值。当个体违反电流和电压的约束条件时，由于惩罚因子取的比较大，其适应度值将非常的低，从而很容易在进化过程中被淘汰。

4 遗传算法与局部寻优算法的混合策略
    在基本遗传算法中，存在着局部搜索能力差、收敛速度慢的缺点。如果在遗传算法框架中加入适当的基于邻域的局部搜索机制，使遗传算法与传统的、基于问题知识的启发式搜索技术相结合构成一种全局和局部搜索相结合的混合遗传算法，则可以保证在种群进化的每一代，算法的解都是局部最优解，再通过竞争从局部最优解中选择产生出优良解。
    本文对经过交叉和变异后的染色体执行连续多次的“连支前插”操作，来寻找染色体对应解所在局部解空间的最优点。首先通过解码器将染色体解成支撑树的形式T={t1t2t3t4...tn,l1l2...lm}。事实上树支集合内的排列排序和连支集合内的排列顺序的改变对于配网的结构都不产生影响，即适应度是不发生变化的，只有当连支与自己所在环内的其它树支发生交换，也就是发生了支路交换，才对网络结构产生影响；连支前插法，就是将连支向前插入至树支区内，例如将组合T中的连支l1向前插至树支t4的前面，T的组合变成{t1t2t3l1t4...tn,l2...lm}的形式，这样将由于先加入而变成树支，同一环内排在最后的树支将变成连支，因此实现了支路交换。
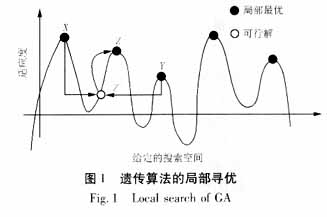
    本文使用的“连支前插”是一种爬山行为(朝着改进的方向)和连续多次的“前插”操作，如果“前插”使串的适应度提高，则执行操作，如此反复，直至不能再前插为止，最后将重新形成组合替代原来的染色体。这一操作实际上使给定的串改良到它的局部极点，这种局部爬山能力与基本遗传算法的全局搜索能力相结合在实验中显示了良好的效果。如图1，算法通过局部寻优算子来修复通过杂交和变异产生的新个体，使它到达局部最优点。图1中父代个体X和个体Y产生出子代个体Z′，通过局部寻优产生出最终个体Z。

5 配网重构的混合遗传算法流程
　　在给定配电网络和数据后，应用本算法求解最优运行方案的步骤如下：
　　a.算法首先读入原始数据进行初始化，设定遗传算法的最大进化代数，群体规模N，代沟G,染色体长度，杂交概率，变异概率等参数。
　　b.采用支路整数编码方法随机产生第一代的初始种群作为父代。并对初始群体的个体进行解码，调用潮流计算程序，计算个体适应度及群体平均适应度。
　　c.基于赌轮选择机制从交代中选择适应度较高的个体进行交叉操作，产生新一代个体。
　　d.对子代个体执行变异操作。
　　e.对子代个体执行“连支前插”操作，使个体得到进一步的改良。
　　f.重复步骤c,d,e，直到子代个体数达到N*G个。
　　g.执行代间更新操作，从父代中复制N*(1-G)个的适应度最高的个体补充到子代中。
　　h.计算子代个体适应度及群体平均适应度，并将子代作为下一轮进化的父代。
　　i.当算法达到预先设定的最大进化代数，算法将结束，并输出适应度最高的个体所对应的网络方案。否则转到步骤c，继续进行进化。

6 算例分析
　　本文算例采用一个33节点、5联络开关的配电网测试系统[4]，如图2所示。

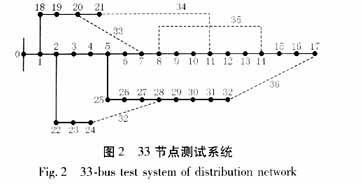
　　5个常开联络开关分别位于支路7～20、11～21，8～14，17～32，24～28上，假设所有支路都装有分段开关，按照文中的编码方法，电源支路不参与重构，一直是闭合状态，不参与编码，因此染色体长度为35，群体规模取50个，交叉概率取0. 6，变异概率取0. 01。运算程序后，最优重构方案为合上支路7～20、11～21，8～14，17～32上的分段开关，断开6～7，8～9，13～14，31～32上的分段开关。表1给出了运算结果并与文献4的算法计算结果进行了比较。

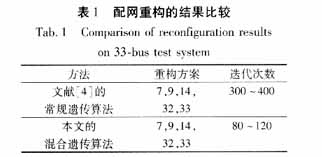
　　本文算法与文献[1]-[4]所述算法相比，其收敛性能有了很大的提高。采用文献的基于二进制编码的遗传算法，在同样的算例上常常要进行到300多代才能收敛，而采用本算法进行到40多代就发现最优个体，在100代左右其平均适应度逐渐收敛于最优，同时相对于文献[1]-[2]，本文在每一代的计算效率也有很大提高。

7　结论
　　在采用遗传算法来解决配网重构中的大规模组合优化问题时，本文采用支路整数编码方法实现基因编码和基于构造支撑树方法的译码器设计方法，避免了生成不可行解的情形，减少了算法的无效搜索，提高了计算效率。同时本文还提出了基于图论的连支前插法的局部寻优算法，将它作为一个局部寻优算子加入到算法中，提高了算法的局部寻优性能，加快了算法的收敛速度。算例结果表明这种方法是可行、有效的。