电力寡头垄断市场的均衡分析

电力市场是一个不完全竞争的市场，模拟这类市场成员策略使用较多的模型有古诺模型、供应函数均衡模型等。本文根据电力市场的特点，提出一种新的博弈模型来模拟发电商的策略行为，推导了该模型的纳什均衡解。最后通过算例比较了该模型与现有模型均衡解的区别，并分析了电力需求弹性和发电容量约束等因素对市场均衡状态的影响。
　　关键词：寡头垄断市场；纳什均衡; 模型；需求弹性；容量约束

Analysis of Equilibrium in OligopolisTIc Electricity Market

Yuan Zhiqiang Deng Chaoping Jiang Chuanwen Hou Zhijian 

(Electric Power Department of Shanghai Jiaotong University 200030)

　　Abstract: The pracTIcal electricity market is an imperfect compeTITIon market and some models, such as Cournot and supply function equilibrium, are employed to simulate the strategies of suppliers. In this paper, a new oligopolistic game model is put forward to simulate the strategies of power suppliers. The formulae of Nash equilibrium are achieved based on complete information. The results of Nash equilibrium are compared with other game models and the impacts of demand elasticity and generation constraints on Nash equilibrium are analyzed. 
　　Key words: Oligopolistic electricity market; Nash equilibrium; Model; Demand elasticity; Generation constraints


1 引言
　　目前的电力市场是一个寡头竞争的市场，研究这类市场的模型主要有古诺(Cournot)模型、Bertrand模型和供应函数模型[1]。文献[2]全面介绍发电市场的竞争行为，指出在完全竞争的市场下发电方为获得最大利润应该按边际成本报价，给出了发电市场的Cournot和供应函数均衡模型。文献[3]用Stackelberg模型模拟了市场参与者的投标策略。文献[4]中提出了不完全信息下电力市场发电商的投标策略问题。本文根据电力市场的特点，认为电力市场中的发电商由领导者、跟随者和价格接受者组成，相应提出适用于联营模式下的电力市场的一种新的模型来模拟寡头垄断的电力市场，给出了该模型的纳什均衡解，并通过算例比较了该模型与现有模型均衡解的区别，同时分析了电力需求弹性和发电容量约束等因素对市场均衡状态的影响。

2 模型的纳什均衡策略
　　电力市场中存在着各种类型的发电商，他们的竞争策略将根据其生产成本、市场份额等因素来决定，其中小型发电商往往会作为价格接受者、中型发电商作为跟随者、大型发电商作为领导者来进行生产。尽管在市场中充当的角色不同，然而各发电商的目的均是使其自身的收益最大化。
　　设电力逆需求函数为线性函数，记为：
   

其中：p为电价，r、s为逆需求函数的截距和斜率，qi为第i个发电商的发电量，N为发电商个数。
　　发电商的利润最大化问题为：
　

　　假设电力市场中前L个发电商作为领导者，第L+1至第M个发电商作为跟随者，最后(N-M)个发电商作为价格接受者。
　　作为价格接受者的发电商，认为其策略行为不会影响市场电价，即认为市场电价独立于该发电商的发电量，他们按边际成本等于市场电价组织生产。而作为跟随者的发电商，与作为价格接受者的发电商的区别在于该类发电商认为其策略行为会影响到市场电价，然而他们认为作为领导者的发电商会首先选择产量，而他们作为尾随企业将通过估计的作为领导者的发电商的发电量来选择自身的产量水平。同时，作为领导者的发电商将首先选择产量，并认为作为跟随者的发电商的发电量是其产量的函数。
　　作为价格接受者的发电商，为了最大化自身利润，其目标函数为： 
　

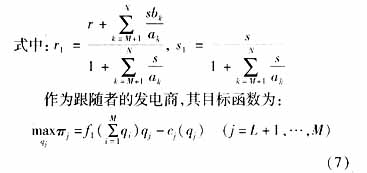
　　 其利润最大化的一阶条件为：


　　相应所有跟随者最优发电量总和为：
　
　


　　市场均衡电价以及相应的各发电商的发电量、总发电量分别为：

　
3 考虑发电容量约束时模型的均衡解
　　 上述模型的反应函数没有考虑到发电约束。当考虑发电约束时，如果由不考虑约束情况计算得到的发电商i的发电量qi超过极限时，则将发电商的发电量设为极限值。即：
　
　　式中U-T、V-U分别为发电量越上限和越下限的发电商数。qimax、qkmin分别为发电商出力的上、下极限。
　　根据剩余需求函数再次计算没有越限的发电机组的发电出力。若仍有发电商出力越限，则利用(16)、(17)计算剩下没有越限的发电商所面临的剩余需求函数，重复计算直到没有发电商出力再次越限为止。需要注意的是，当发电商i的发电量qi超过下限时，如果满足pqimin-ci(qimin)≤0，则令qi=0。

4 算例分析
　　以IEEE6机系统为例对本文模型的市场均衡电价和最优发电量进行了计算，并将本文所提出模型的市场均衡结果与现有模型的结果进行了比较，分析了电力需求弹性和发电容量约束等因素对市场均衡状态的影响。
　　本文假定市场逆需求曲线为，
 
　　各发电商的成本系数见表1。其中发电商1、2为领导者，3、4为跟随者，5、6为电价接受者。此时用本文模型模拟电力市场竞争的均衡结果见表2和表3。在用于对比的模型中，Forchheimer模型发电商1、2为领导者，其余发电商为价格接受者，Stackelberg模型发电商1、2为领导者，其余发电商为跟随者。

　　从表中结果可以看出，当不考虑发电约束时，由于本文模型的价格接受者少于Forchheimer模型而多于Stackelberg模型，因而计算得到的市场电价高于完全竞争的模型和Forchheimer模型而低于Stackelberg模型和Cournot模型。当考虑发电约束时，由于本文模型作为价格接受者的发电商6超越上限，因而使得剩下的参与竞争的发电商数目少于Stackelberg模型参与竞争的发电商数目，因而此时采用本文模型计算得到的市场电价高于Stackelberg模型计算的电价。
　　为分析需求弹性对发电商均衡策略的影响，本文考虑了逆需求曲线斜率s放大0.2~2倍的情况，此时不考虑发电约束时五种模型的均衡电价计算结果见图1，考虑发电约束时均衡电价计算结果见图2。

　　从图中可见，五种模型的均衡电价均随逆需求曲线斜率的增加而下降，不考虑发电约束的均衡电价低于考虑约束时的均衡电价。当不考虑发电约束时，Cournot模型的电价最高，其他依次为Stackelberg模型、本文模型、Forchheimer模型和完全竞争模型。如果考虑发电约束，当需求弹性较大时(对应于s较小)，由于所有发电商出力越上限，因而各模型的均衡电价均相同并且较高，随着需求弹性的下降，Forchheimer模型、Stackelberg模型和本文模型的电价大小次序交替变化，但仍然是Cournot模型的电价最高，完全竞争模型的电价最低。

5 结论
　　 本文根据电力市场的特点，提出了一种新的博弈模型来模拟发电商的策略行为，推导了该模型的纳什均衡解。仿真结果表明，不考虑发电约束时，该模型的电价高于完全竞争模型和Forchheimer模型的电价而低于Stackelberg模型和Cournot模型的电价。考虑约束时，上述模型电价大小次序会随着需求弹性的变化而变化。当需求弹性较低时，所有模型的电价大小会随着需求弹性的下降而迅速下降，最后电价趋于稳定。应该指出，本文中提到的所有模型均为本文所提出模型的一种特殊情况：当作为领导者和跟随者的发电商均为价格接受者时，本文模型则成为完全竞争模型；当作为跟随者和价格接受者的发电商的策略均与作为领导者的发电商策略行为一致时，本文模型则成为Cournot模型；当作为价格接受者的发电商成为跟随者时，本文模型则为Stackelberg模型；当作为跟随者的发电商成为价格接受者时，本文模型则为Forchheimer模型。