作者：欧书俊，张国俊，王姝娅，戴丽萍，钟志亲（电子科技大学 电子薄膜与集成器件国家重点实验室，四川 成都 611731）

本文针对一字型悬臂梁RF MEMS开关，提出了两种降低驱动电压RF MEMS开关的方法，分别为：增大局部驱动面积和降低弹性系数。根据这两种方法设计了4种形状的悬臂梁开关，分别为增大局部驱动面积的十字型梁，降低弹性系数的三叉戟型、蟹钳型和折叠型梁。在梁的长度、厚度和初始间隙等参数一致的情况下，通过CMOSOL软件建模仿真得到了这4种悬臂梁的驱动电压，分别为7.2 V、5.6 V、3.8 V和3.6 V。相比于驱动电压为9 V的一字型悬臂梁，优化后的这4款开关可以降低驱动电压。并且低弹性系数方面，比增大局部驱动面积的开关效率要高。

RF MEMS开关无论是在民品还是军品都有着广泛的应用，相对于传统的PIN二极管开关和GaAs开关有着巨大的优势，并具有低插入损耗、高隔离、线性度极好、低功耗、体积小和低成本的优点［1-2］。

目前，RF MEMS开关存在着较高的驱动电压，静电MEMS开关通常需要高达30~80 V的驱动电压［3］。在通讯系统中，就需要利用变压器将输入很低的控制电压提升到所需的驱动电压，这限制了RF MEMS开关的应用以及单片式微波集成电路（MMIC）的集成。如果降低了MEMS开关的驱动电压，不但可以扩大RF MEMS开关的应用范围，而且可以增强开关的性能，因此低驱动电压的开关也能应用于MMIC中［4］。

悬臂梁开关相比于固支梁开关具有更低的驱动电压。本文在现有研究的基础上，提出了增大局部驱动面积和低弹性系数的悬臂梁来减小驱动电压的方法。通过CMOSOL软件建模对不同形状的悬臂梁开关进行仿真验证。在梁的长度、厚度和初始间隙等不变的情况下，得到了通过增大局部驱动面积和降低弹性系数的悬臂梁可以降低驱动电压，并且低弹性系数的悬臂梁对降低驱动电压的效率更高。

1 开关工作原理

图1为悬臂梁开关原理示意图，其中悬臂梁左端固定，右端是可动的悬空结构。悬臂梁和驱动电极之间形成平行板电容，当驱动电极未施加电压时，悬臂梁处于初始位置，开关处于断开状态；当驱动电极施加电压时，梁上会产生静电力，并在静电力的作用下向下运动，在静电力足够大时，悬臂梁的触点金属和信号电极接触，左右信号电极导通，此时开关处于导通状态。为了避免开关导通时直流驱动电路对微波通路的影响，通常在驱动电极上沉积一层绝缘层。

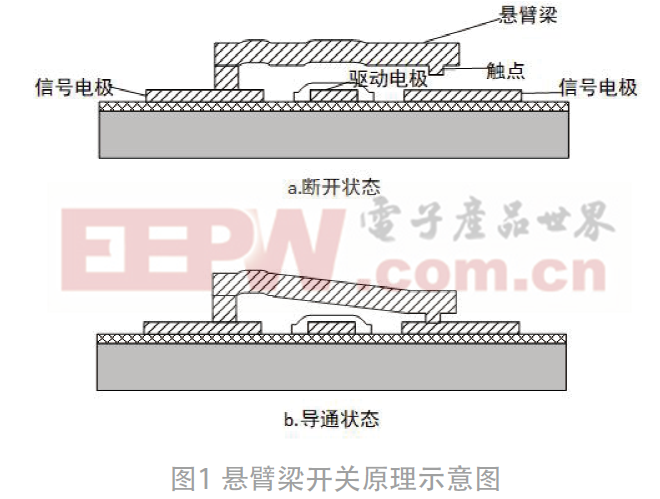
由射频微系统的相关知识可知：梁的不稳定状态g和驱动电压Vp分别为［5］：

其中：g为悬臂梁到驱动电极之间的间隙，g0为初始间隙。悬臂梁宽度ω，驱动电极宽度W。

2 一字梁的弹性系数

当驱动电压升到Vp 时，悬臂梁在静电力作用下会快速下拉，此时触点金属和信号电极接触，则信号导通。从式（2）可以看出，悬臂梁的弹性系数 k是计算悬臂梁的驱动电压的关键，接下来我们对弹性系数的 k值进行分析。

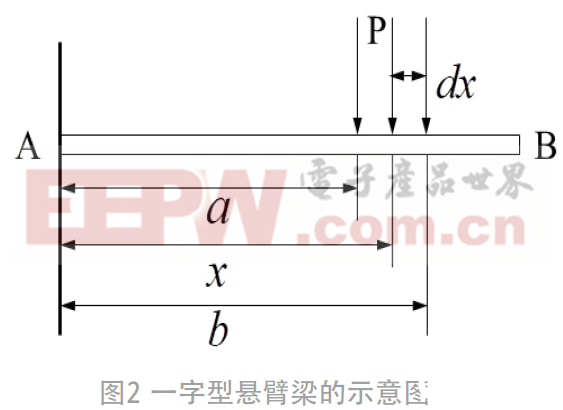
如图2 所示， 当一字型悬臂梁的任意位置受到均布载荷时［6］，由材料力学知识可得： dP =ξ dx ，

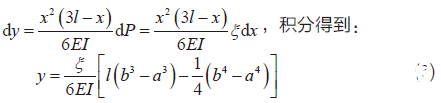
其中：ξ为单位长度的载荷大小，y为悬臂梁的挠度，E为梁材料的弹性模量，l为梁的长度，I为转动惯量，对于矩形截面，则I=ωt3/12，其中t为梁的宽度。

在静电力载荷的作用下悬臂梁的变形程度很小，可以用胡克定律F=kx来描述，即

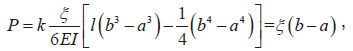
解得：

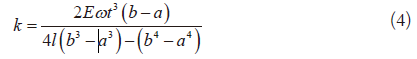
当载荷均布在整个梁上时， 即 a=0、b=1，k=2Eωt3/3l3。对于共面波导（CPW）传输线，载荷在梁下方正中间位置，宽度为梁长的1/3，即a=l/3、b=2l/3，此时k=54Eωt3/69l3。将k带入式（2）可以得到理想情况下的驱动电压公式。

3 开关的机电仿真

由于CPW的传输优势，RF MEMS开关通常选择CPW的传输模式［7］，但是k的增加导致了驱动电压的增加，所以在CPW传输模式中设计具有低弹性系数的悬臂梁显得至关重要。

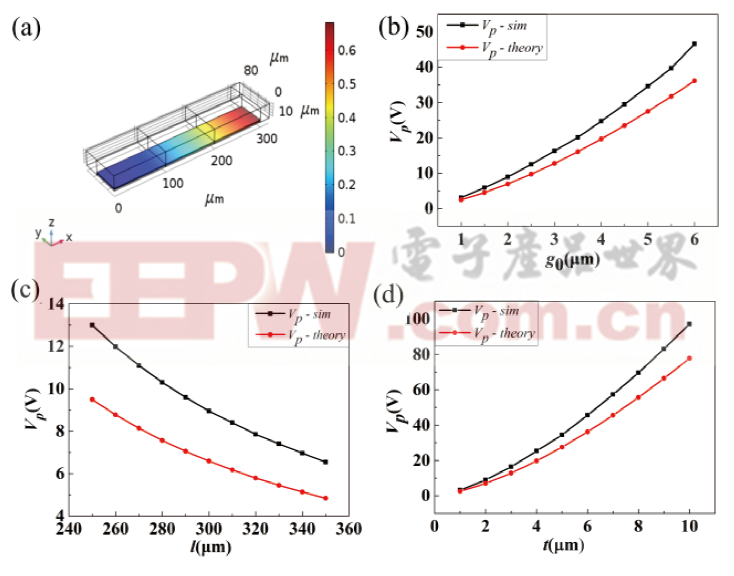
图3为一字型悬臂梁驱动电压的仿真结果。当梁的长度l=300 μm、梁的宽度t=2 μm、悬臂梁到驱动电极之间的初始间隙g0=2 μm时，悬臂梁在9 V驱动电压下的Z向位移图如图3（a）所示。图3（b）~3（d）分别为改变不同参数情况下得到的驱动电压图，从中可以得到理论和仿真结果的变化趋势一致，但在数值上理论计算小于仿真结果，主要原因是仿真时可在梁的周围设置空气层，梁产生形变过程中会影响空气层中电场分布，因此增大了驱动电压的仿真结果。

图3 （ a ） 悬臂梁在9 V驱动电压下的Z向位移图（l=300 μm，t=2 μm，g0=2 μm）；一字型悬臂梁驱动电压的理论计算和仿真数值对比图，（b） 当l为变量，（t=2 μm、g0=2 μm）；图（c） t为变量，（l=300 μm、g0=2μm）；（d） g0为变量，（l=300 μm、t=2 μm）。

针对一字型悬臂梁模型进行了改进，分别提出了4种优化模型，并采用COMSOL软件对4种开关模型进行机电仿真分析，由于金的杨氏模量为70 GPa相对较小，泊松比ν为0.44，在几何参数一致的情况下具有相对较小的弹性系数，所以选择金作为悬臂梁材料。与图3（a）中的一字型悬臂梁模型对比，图4（a）为增大局部驱动面积的十字型悬臂梁模型；图4 （b）~（d）分别为未增大局部驱动面积但是降低了弹性系数的三叉戟型、蟹钳型和折叠型的悬臂梁模型（左边一列为4种优化的悬臂梁模型的俯视图，其尺寸都标注在图中，右边一列为左边模型对应的悬臂梁在不同电压下发生的形变量）。当Z方向的形变量下降了g0/3 （约为 -0.7 μm） 时对应的电压为驱动电压，从形变图中可以得到，十字型悬臂梁的驱动电压为7.2 V；三叉戟型的驱动电压为5.6 V；蟹钳型的驱动电压为3.8 V；折叠型的悬臂梁的驱动电压3.6 V。对不同的模型施加其对应的驱动电压得到的Z向位移分布如图5所示，其悬臂梁的自由端在驱动电压下向下运动，颜色标注为模型发生的形变量的大小。

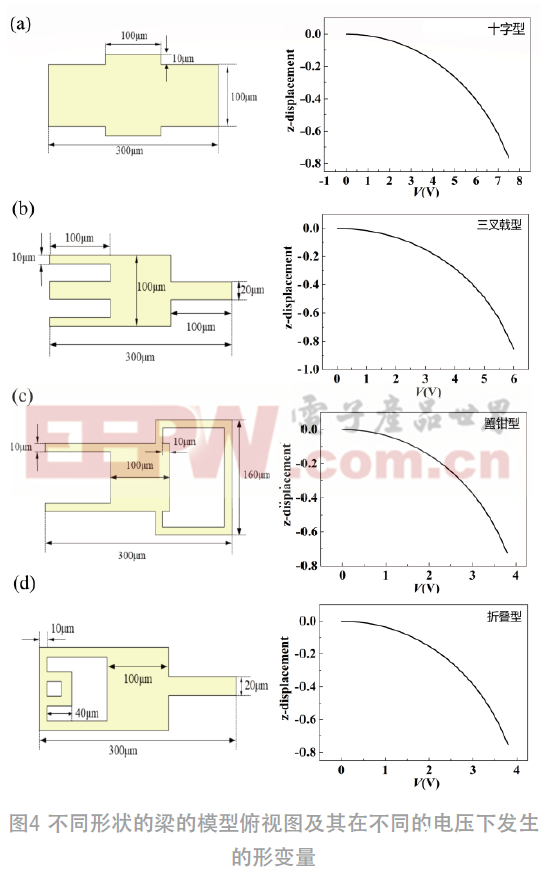
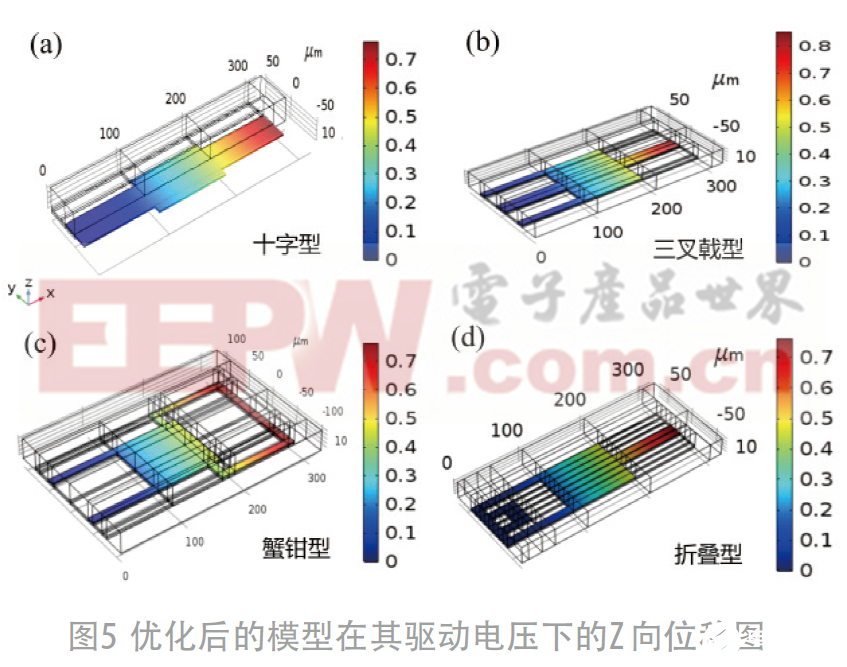
表1 中列出了不同形状的梁在不同驱动电压下的Z向位移量的具体值，并给出了不同梁的驱动电压，验证了增大局部驱动面积和降低弹性系数的悬臂梁可以减小驱动电压。然后在相同梁长的情况下对比了通过上述两种方法设计的悬臂梁的驱动电压大小，由对比结果可知，在梁长、厚度和初始间隙等参数一致的情况下，低弹性系数的梁对降低驱动电压的效率比局部增大驱动面积要高很多。

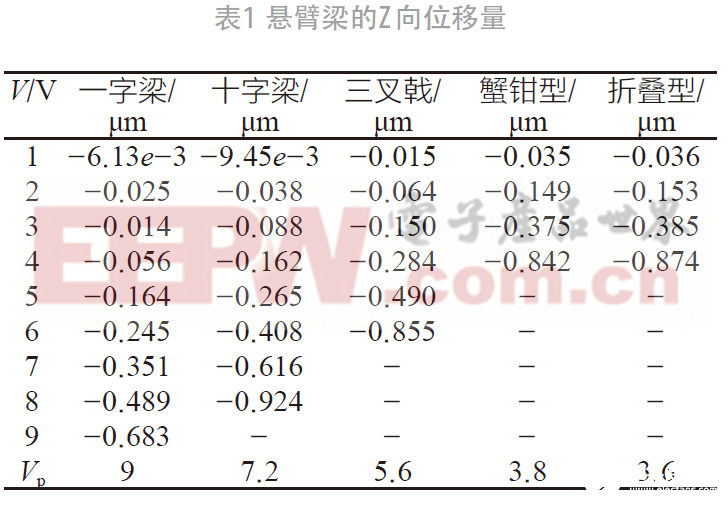
注：表中“-”意为位移量已经远大于临界不稳定状态的位移，所以没有统计。

4 结论与分析

通过理论分析和仿真，并与传统的一字型悬臂梁作对比，验证了增大局部驱动面积和降低弹性系数可以减小悬臂梁开关的驱动电压。并且降低弹性系数的悬臂梁比增大局部驱动面积的悬臂梁在降低驱动电压方面更有效。在选择低弹性系数的悬臂梁开关材料时也可以选择弹性模量较大的材料，如多晶硅、氮化硅等硅化物形成单层或者多层结构的梁，这将有利于降低成本以及工艺的可集成性。

参考文献：［1］ REBEIZ G M， MULDAVIN J B. RF MEMS switches andswitch circuits ［J］。 IEEE Microwave Magazine， 2001， 2（4）：59-71.

［2］ MULDAVIN J B， REBEIZ G M. High-isolation CPWMEMS shunt switches. 1. Modeling ［J］。 IEEE Transactionson Microwave Theory and Techniques， 2002， 48（6）： 1045-1052.

［3］ LAI Y L， CHANG L H. Design of electrostatically actuatedMEMS switches［J］。 Colloids & Surfaces A Physicochemical& Engineering Aspects， 2008， 313-314（none）：469-473［ 4 ］ HAR V E Y S 。 Newma n 。 R F MEMS s w i t c h e s a n da p p l i c a t i o n s ［ C ］ / / R e l i a b i l i t y P h y s i c s S y m p o s i umProceedings， 2002. 40th Annual. IEEE， 2002.

［5］ BEBEIZ G M. RF MEMS理论·设计·技术［M］。黄庆安， 廖小平，译。 南京：东南大学出版社， 2005.

［6］ 刘庆玲。不同加载方式对微悬臂梁弹性系数的影响［J］。机械设计与研究， 2008， 24（3）： 49-51.

［7］ MILANOVIC V， GAITAN M， BOWEN E D， et al.

Micromachined microwave transmission lines in CMOStechnology［J］。 IEEE Transactions on Microwave Theory &Techniques， 2002， 45（5）：630-635.

（注：本文来源于科技期刊《电子产品世界》2020年第07期第73页，欢迎您写论文时引用，并注明出处。）